Keywords
Abstract
Quantum dots are the most exciting representatives of nanomaterials. They are synthesized using advanced methods of nanotechnology pertaining to both inorganic and organic chemistry. Quantum dots possess unique physical and chemical properties; therefore, they are used in very different fields of physics, chemistry, biology, engineering and medicine. It is not surprising that the Nobel Prize in chemistry in 2023 was given for discovery and synthesis of quantum dots. This review addresses modern methods for the synthesis of quantum dots and their optical properties and practical applications. In the beginning, a short insight into the history of quantum dots is given. Many gifted scientists, including chemists and physicists, were engaged in these studies. The synthesis of quantum dots in solid and liquid matrices is described in detail. Quantum dots are well-known owing to their unique optical properties; that is why the attention in the review is focused on the quantum-size effect. The causes for fascinating blinking of quantum dots and techniques for observation of a single quantum dot are considered. The last part of the review describes mportant applications of quantum dots in biology, medicine and quantum technologies.
The bibliography includes 772 references.
1. Introduction
In the second half of the 20th century, active development of chemical processes for fabrication and doping of multicomponent glasses, nanoparticle synthesis by colloidal chemistry techniques[1-7] and epitaxial growth of films and nanostructures (in particular, by molecular-beam and metal-organic vapour-phase epitaxy)[8-13] resulted in the appearance of a fundamentally new class of nano-objects, quantum dots (QDs).
The term ‘quantum dot’ was proposed much later than the discovery. Reed introduced this term while considering the electron transport in a three-dimensionally confined semiconductor quantum well[14] and used it in relation to the epitaxial quantum dots formed as ordered three-dimensional coherently strained (that is, dislocation-free) nanometre-sized islets formed upon self-organization effects in the molecular-beam and vapour-phase epitaxy from organometallic compounds (Figure 1a)[10-12].
Quantum dots are separate (isolated from one another) semiconductor nanocrystals (most often, binary or ternary) with the size approximately equal to or smaller than the radius of the Wannier – Mott exciton in the corresponding substance. The Wannier – Mott exciton radii for various semiconductors vary from a few nanometres to a few tens of nanometres[2].
A fundamental feature of the QD energy structure is size quantization effect, which means that the decrease in the linear size of the semiconductor crystal down to several nanometres is accompanied by an increase in the energy distances both between the neighbouring states of the valence band occupied with electrons and between the vacant states of the conduction band by a value exceeding \( kT \) (Figure 2).
The quantum size effect present in QDs provides the possibility of controlling the energy, absorption, transport and luminescent properties by varying the size and geometry of nanocrystals without changing their chemical composition[1-7].
Currently, colloidal QDs of a variety of compositions are being successfully produced. The quantum dots that are synthesized, studied and practically used most often are made of semiconductors AIIBVI (CdSe, CdS, ZnS, ZnSe, ZnTe CdTe, HgS, HgSe, HgTe), AIIIBV (GaN, GaAs, InP, InAs), AIBVI (Ag2S, Ag2Se, Ag2Te), AIBVII (CuCl, CuBr, AgI) and AIVBVI (PbSe, PbS, PbTe, SnTe, SnS). Quantum dots of more complex compositions (InGaAs, CdSeTe, CdHgTe, ZnSeS, ZnCdSe, ZnHgSe, ZnSeTe, CuInS2, CuInSe2, CuGaS2, AgInS2, AgInSe2, and AgGaS2) are also known, including perovskite QDs [CsPbX (X = Cl, Br, I)][1-5, 15-19]. It is the semiconductor colloidal quantum dots that are the subjects of the present review.
Prerequisites for the fabrication of QDs appeared immediately after the development of quantum mechanics and consideration of the state quantization problem for a microparticle (electron) in a one-dimensional potential well of both finite and infinite depths[20, 21]. Back in the 1930s, it was noted that qualitatively new effects not inherent in bulk samples appear in semiconductor and semimetallic films with the thickness L ~ 100 nm (and thinner)[22, 23]. However, systematic study of the quantum size effect in semiconductors was initiated much later, in the 1960s, by Sandomirskiĭ, Tavger and Demikhovskiĭ. It was predicted that the fundamental absorption edge in thin crystal films should shift to blue region as the film thickness decreases[24, 25]. The development of molecular beam epitaxy methods led in a few years to the design of semiconductor quantum wells and superlattices[9, 10].
The first brief communication describing empirical observation of the change in the band gap width with decreasing size of AIIBVI nanocrystals grown in glasses appeared somewhat later[26]. No data that would support these statement were given in the publication and, what is more important, the interpretation of the observed effect was incorrect.
In 1980, Aleksey Ivanovich Ekimov and Aleksey Arkadievich Onushchenko, who worked at the S.I.Vavilov State Optical Institute and had graduated from the E.F. Gross Department of Molecular Physics, Faculty of Physics, Leningrad State University, fabricated the first CuCl QDs, at a suggestion of Viktor Alekseevich Tsekhomsky, Doctor of Chemical Sciences, Head of the department engaged in the development of copper halide photochromic glasses. The first quantum dots were CuCl nanocrystals grown during diffusion-controlled phase separation of a supersaturated solution in glasses under variable conditions such as synthesis temperature and time of heat treatment (Figure 1b)[27, 28]. Valery Viktorovich Golubkov, Doctor of Chemical Sciences, employee of the I.V.Grebenshchikov Institute of Silicate Chemistry of the Academy of Sciences, future honoured scientist of the Russian Federation, established the formation of CuCl and CdS nanocrystals with a size of 3 nm or more using small-angle X-ray scattering. A decrease in the size of grown nanoparticles induced a blue shift of exciton absorption bands, which was interpreted as a quantum size effect[27-30].
In the same period of time, Soviet physicists Aleksandr Lvovich and Alexei Lvovich Efroses reported the first analytical consideration of the quantum mechanical problem of light absorption in a small semiconductor sphere using the effective mass approximation[31]. Experimental studies of quantum size effect for glasses containing copper halide and cadmium chalcogenide nanocrystals started at the same time. A series of publications demonstrated the quantum size effect in the optical absorption spectra of CuCl, CuBr, CdSe, CdS and CdSSe QDs[32-39]. As the nanocrystal size decreased from 20 to 1.5 nm, an increase in the blue shift of narrow absorption peaks was observed at low temperatures. The photoluminescence spectra of CuCl and CuBr nanocrystals exhibit very intense peaks located at 2 – 5 meV distance from the absorption peaks (below referred to as Stokes shift), while in the case of CdSe and CdS nanocrystals of 1.5 – 6 nm size, apart from the narrow peaks with a Stokes shift of 2 – 25 meV, broad structureless luminescence bands were observed.
Distinctive features of the formation of QDs in glasses are high synthesis temperatures (473 – 973 K, 200 – 700 °C), a significant size variation of the formed nanocrystals, and the absence of possibilities for additional passivation and functionalization of QD interfaces or construction of hybrid nanostructures with organic molecules, fullerenes, etc.
A fundamental step towards more facile processes of QD synthesis, providing a considerable expansion of the scope of potential applications, was made by the development of colloidal synthesis in hydrophilic and hydrophobic media (Figure 1c), in particular in polymers (Figure 1d).
The first successful attempts to obtain colloidal solutions containing nanocrystals with properties differing from the similar properties of bulk crystals were made almost simultaneously with QD fabrication in glasses[40-43]. The facts demonstrating the size effect in the absorption and luminescence spectra were reported[40, 41], but they were not analyzed or explained in detail.
The development of colloidal chemistry of QDs in polar media started with the studies of Brus and Rossetti in 1982[42, 43]. They used aqueous colloidal CdS nanocrystals to attain a greater surface area needed to study organic oxidation and reduction reactions on the surface of photoexcited semiconductors. The variations of the optical properties of synthesized nanocrystals that took place on storage were interpreted as changes in the band gap width caused by Ostwald ripening and increasing particle size. The results were correctly interpreted using modelling of the quantum size effect in the framework of the effective mass approximation[44-46]. A new approach, wet synthesis, made it possible to simplify the procedures and conditions of QD synthesis and to eliminate the glass matrix and single-crystalline substrates (in the case of epitaxial QDs) and provided access to interfaces and possibility of further functionalization. A typical feature of QDs synthesized using mainly phosphates and amines for passivation is relatively low quantum yield and selectivity of luminescence bands. The use of thiol passivation resulted in some improvement of parameters of QD luminescence[19, 47, 48]. However, the attained degree of dispersion of QDs in an ensemble precluded gaining in-depth understanding of the QD exciton structure and observed spectral features. These drawbacks delayed the active use of the unique size-dependent properties of QDs, especially their luminescence. There also remained difficulties of the preparation of small (1.5 – 2.5 nm) QDs. A progress along this line was important for understanding of the fundamental problem of substance evolution from molecules to bulk crystals. The fabrication of small-size (1.5 – 2.5 nm) colloidal QDs was started in the second half of the 1980s by Alivisatos and Bawendi, post-graduate students under the supervision of Brus, in close cooperation with Steigerwald, who specialized in organometallic synthesis[49, 50]. These studies initiated the next major step in the development of synthesis of QDs with specified size-dependent absorption and luminescent properties. In 1993, Bawendi and his post-graduates Norris and Murray implemented a new organometallic synthesis[51]. The synthesis in high-boiling solvents [trioctylphosphine (TOP), trioctylphosphine oxide (TOPO), tributylphosphine (TBP) and trioctylphosphine selenide (TOPSe)] was based on pyrolysis of organometallic reagents, which were rapidly injected into hot coordinating solvents; this ensured the appearance of numerous identical crystallization nuclei. A decrease in the solution temperature as a result of injection provided controlled uniform growth of QDs without formation of new nuclei. By slow growth of nanocrystals attained by high-temperature annealing (473 – 573 K, 200 – 300 °C) in a coordinating solvent, it was possible to minimize the concentration of defects and increase the uniformity of the crystal structure of the resulting QDs[51]. The variation of conditions of colloidal synthesis made it possible to synthesize QDs of various diameters and shapes, to control their size and, what is most important for practical applications, to attain bright and stable luminescence (with a quantum yield of ~70 – 80%) with size-dependent characteristics (position of the maximum, intensity, luminescence quantum yield and luminescence lifetime)[4, 51].
The appearance of new techniques of colloidal QD synthesis stimulated theoretical studies in physics and physical chemistry of the size effect. The progress in the size effect description using the method of effective mass[31] started with theoretical models developed by Brus[44-46]. Numerous studies[52-72] resulted in the formation of views explaining the experimental regularities of the quantum size effect in the optical absorption and luminescence spectra of colloidal QDs, including the temperature effects and exciton dynamics. The development of wet synthesis of various QDs, which can be obtained over a broad range of sizes using the same technique, demonstrated significant discrepancies between the experimental and theoretical size dependences of the optical absorption spectra[66-72]. It became evident that it is necessary to take into account the non-parabolicity of the energy bands and to adequately use crystalline theory for 1 – 2 nm QDs.
A considerable progress in the understanding of quantum size effect in QDs was gained due to ab initio calculations[73-75]. These calculations were actively performed in the last decade with the growth of computing capabilities that provide calculations for QDs of 3 – 5 nm size. First of all, ab initio calculations confirmed the views of discrete energy structure of QDs established using the effective mass approximation and considerably corrected these views[76-78]. In addition, the basic views on the physicochemistry of localized states in QDs started to form, related to both their non-stoichiometry and impurity atoms and passivating agents (organic molecules, semiconductor shells, dielectrics and polymers) and also to mechanisms of their participation in photophysical and photochemical processes[79-86].
By this time, it was already clear that many properties of QDs, especially luminescent properties, are determined not only by the nanocrystal and matrix nature but also by the state of interface between them[87, 88] (see а). Despite the substantial progress in the synthesis of perfect QDs with highly selective exciton luminescence peaks, additional broad luminescence bands were observed for many QD compositions. It was established that characteristics of this luminescence are related to the type of organic agents used for passivation and perfection of passivating shells, while luminescence is caused by the capture of excitons to interface defect levels. This gave rise to a new trend, often called Stokes shift engineering, which is engaged in finding the optimal conditions for passivation of nanocrystal surface, selection of passivating agents and control of the non-stoichiometry of QD compositions. However, the central problem determining the development of this trend is elucidation of the nature of Stokes shift[89-91]. Therefore, active investigations of QD exciton structure and dynamics are of great importance[56, 92-95]. In some cases, a simplified interpretation of the Stokes shift based on molecular theory (configuration coordinates) in luminescence is used[96-98]. However, the decrease in the QD size variability attained in the method of synthesis proposed by Murray et al.[51] revealed abnormal features in the QD exciton dynamics that are not fit into the used models[99]. This stimulated the formation of another approach taking into account the band structure of the compound from which the nanocrystals were prepared and the exciton fine structure[56, 93, 95].
The development of views on the nature of the Stokes shift and exciton dynamics for a wide range of QD compositions is still a relevant and not finally solved problem, since the model substantiated for CdSe QDs is not versatile. For example, for compounds AIVBVI, such as PbS or PbSe, the band structure is markedly different and requires considering the 64-fold degeneracy of the exciton and delocalization of the exciton wave function, because it efficiently interacts with all optical and acoustic phonon modes[95].
For luminescence arising upon optical transitions at the structural defect levels, substantiation of the recombination model remains the key problem. This problem has been addressed in a number of studies[100-107]. In some cases, the authors were able to justify the mechanism of luminescence at structural impurity defect levels in QDs by analyzing exciton dynamics using femtosecond transient absorption spectroscopy, photon echo, pico- and nanosecond luminescence kinetics and analysis of the appropriate size dependences.
The above problems indicate the necessity of development of this field of materials science in close connection of chemical techniques of QD synthesis and physical models describing the unique properties of QDs. Apparently, the most important achievement of the colloidal QD chemistry was the development of two key approaches to the synthesis of QDs with size-dependent spectral, luminescent, transport and other properties in polar and non-polar media. One approach includes the preparation of hydrophilic colloidal solutions of QDs stabilized by water-soluble polymers, surfactants and other hydrophilic molecules[47, 103, 104, 108-110]. According to the other approach, hydrophobic colloidal QDs are obtained by high-temperature organometallic synthesis in high-boiling solvents (Figure 1c,d)[51, 87, 88, 111-113].
The synthesis in reverse micelles has also been markedly advanced; this method includes elements of both above approaches: the formation of a water – oil type suspension and stabilization of the resulting QDs by surfactants (Figure 1e)[114-116]. According to this method, QDs are formed within highly dispersed drops of water. The size of reverse micelles restricts the size of particles synthesized in them.
In order to reduce the influence of non-radiative decay channels of electronic excitation on the luminescence quantum yield and to increase the QD photostability, nanocrystals are coated, at the final stage of the synthesis, by a layer of wide-band-gap material, e.g., ZnS or CdS for CdTe, CdSe (core/shell QDs) (Figure 1f )[2, 87, 117]. The shell serves as a barrier for carrier tunnelling into the matrix and reduces the concentration of dangling bonds at QD interfaces.
Thus, the feasibility of most procedures of colloidal synthesis, the specific luminescent properties determined by size-dependent energy structure of QDs and a number of currently established factors affecting the QD luminescence are of primary importance for QD applications; the following applications are discussed most frequently:
— luminescent sensorics of gases, heavy metals and toxic substances[118-122];
— electroluminescence emitters such as organic light emitting diode — quantum dots (OLED-QDs)[123-129];
— luminescent labelling and imaging of tissues and cells in vivo and in vitro in biomedicine[130-148];
— elemental base of photovoltaics (solar cell)[126, 149-156];
— photocatalysts[157-160];
— photodynamic therapy[161-163];
— quantum cryptography[164-168];
— laser technology[169-176];
— luminescence temperature sensors[177-184];
— luminescence pH indicators[185-189];
— optoelectronic devices (systems for the control of light flux intensity, up-converters, active media for higher harmonic generation, etc.)[190-197].
An important distinctive feature of colloidal QDs is the approach to their preparation in which the nanocrystal interfaces are in contact with organic passivating agents. Therefore, colloidal QDs should be treated as inorganic-organic (or hybrid) low-dimensional objects.
The organic component may perform different functions. In some cases, the organic component improves the properties of semiconductor nanocrystals, providing stabilization (passivation) of QD interfaces, hydrophilicity or hydrophobicity of the corresponding colloidal solution, control over the concentration of dangling bonds and, hence, over the quantum yield, lifetime and other characteristics of nanocrystal luminescence[138, 198-201].
Hybridization with functional molecules such as organic dyes, DNA fragments, etc., and with plasmonic nanoparticles markedly expands of the range of hybrid properties arising mainly via interaction between the organic and inorganic components. The QD association with molecules such as organic dyes, DNA fragments, etc. may be implemented as covalent bonding[202, 203], hydrogen bonding[202], dipole — dipole interactions[204, 205] and secondary functionalization effect (Figure 3)[206, 207]. This further expands the range of possible applications in the following fields:
— design of singlet oxygen photosensitizers for the photodynamic therapy[200, 208, 209];
— development of photobactericidal coatings and wound-healing compositions[210, 211];
— fabrication of organic-inorganic charge separation systems[212, 213];
— design of systems for the control of laser radiation parameters[94, 190-197];
— development of biomarkers and sensors[214-219];
— fabrication of single photon sources and quantum computers[220].
The present review is devoted to the diversity of modern methods for the synthesis of semiconductor colloidal quantum dots, details of the electronic structure of quantum dots, optical spectroscopy of size effects, features of exciton dynamics and luminescence mechanisms, effect of defects and interface structure on the exciton spectra and dynamics, effect of crystallization and passivation conditions on the optical properties of QDs and practical applications of QDs.
2. Synthesis of quantum dots
2.1. At the roots: discovery of quantum dots and first results
The techniques used to grow colloidal particles in glass have been known for a very long time. However, the work of Ekimov of 1979, devoted to physicochemical mechanisms of colouring of commercial light filters (Schott) was a turning point in their development. The primary goal of this study was not only to determine the growth mechanisms of colloidal particles in a dielectric matrix, but also to establish their structure and chemical composition. Although commercial colour filters were composed of complex particles based on cadmium sulfoselenides (CdSSe) (Glass is synthesized using a mixture of cadmium sulfide and selenide, which affords particles of CdSSe type ternary compounds. By varying sulfur to selenium ratio, it is possible to obtain yellow to red filters.), Ekimov’s attention was focused on the effect of glass activation with binary copper- or cadmium-based compounds: copper chloride or bromide (CuCl, CuBr) and cadmium sulfide or selenide (CdS, CdSe). As a result, in 1981, copper chloride (CuCl) QDs were synthesized for the first time in a multicomponent silicate glass matrix[221]. Unlike the spectra of non-activated glass, the spectra of activated samples containing chloride and copper ions exhibited two narrow bands after heat treatment. The observed spectrum coincided with the absorption spectrum of bulk CuCl crystals, which was caused by excitation of excitons associated with the spin–orbit split valence subbands. This result unambiguously indicated that the colour of glasses of this type is due to crystalline impurities (in this case, CuCl) dispersed in the amorphous glass matrix. In addition, it was found that the position of exciton lines markedly depended on the temperature and duration of sample annealing: the lower the temperature, the more pronounced the blue shift of the optical absorption edge relative to that for bulk CuCl. Subsequently, it was shown by small-angle X-ray scattering measurements that the particle diameter changes from 3.4 to 62 nm as the annealing temperature increases from 773 K (500 °C) to 973 K (700 °C)[33, 222]. Ekimov and co-workers attributed the obtained results to the quantum size effect.
Despite the considerable progress in the studies of the properties of QDs in glasses, investigation of colloidal semiconductor QDs was restricted at that time to their applications in solar energy generation[223-227]. Before Brus and co-workers discovered quantum size effect for CdS particles in 1983[43], they investigated the photochemical processes on the CdS surface by Raman spectroscopy in an aqueous colloidal solution. The aqueous colloidal solutions of CdS for this study were obtained by controlled precipitation after fast injection of the initial components. The authors ascertained that the optical absorption edge of particles depended on the solution lifetime and was blue-shifted as the QD size decreases to 4.5 nm. The particle size increased with time to 12.5 nm, while the absorption edge shifted back to the value corresponding to the band gap of bulk CdS. Relying on these results, Brus applied the effective mass theory to describe the measured shift depending on the size[44, 45]. After Alivisatos joined the Brus’ research team in 1986, they together with Steigerwald developed a process for the synthesis of colloidal QDs[49, 228], using procedures and techniques of organometallic chemistry to remove oxygen: the Schlenk line and glove boxes were adapted for this purpose.
After that, unique behaviour upon a change in the size of semiconductor particles to the nanoscale was discovered for quite a few objects such as ZnS, ZnSe, CdSe and PbS[229-231]. Owing to the efforts of Brus[229, 231, 232, 43-46], Henglein[223, 225, 233], Fendler[227], Grätzel[224, 234] and Nozik[235], CdS QDs became the first semiconductor particles that were used for an in-depth study of physical and physicochemical properties of zero-dimensional objects. Alexander and Alexey Efroses[31] and Brus and co-workers[45, 46, 236] used the knowledge gained for CdS QDs to carry out the first series of theoretical studies for determination of the electronic structure of quantum dots in order to predict and understand their optical properties, which depend on the QD size, structure and size distribution. The history of the discovery and development of the views on the quantum size effect will be discussed in detail in the next chapter.
The key drawback of the above-described methods for the synthesis of QDs in a glass matrix and in solutions is the lack of full control of the nucleation and growth and poor reproducibility. At the end of the 1980s, it was found that Lewis bases form coordination bonds with the surface of cadmium atoms, thus favouring the dispersion of QDs in a solvent volume[228]. The subsequent experiments on the synthesis of CdSe QDs demonstrated that the presence of phosphonic acid impurity in tri-n-butylphosphine oxide plays a crucial role for the preparation of high-quality QDs[112]. In 1993, Murray and Bawendi developed an effective and reproducible method for the synthesis of monodisperse QDs[51]. The high-temperature colloidal synthesis is based on the pyrolysis of organoelement reagents, which are introduced into a hot coordinating solvent (tri-n-octylphosphine or tri-n-octylphosphine oxide) to give CdX nanocrystals (X = S, Se, Te). The proposed method not only complied with the main condition for the formation of monodisperse particles, that is, separation of nucleation and growth processes, but also led to higher crystallinity of the particles[237]. This was possible owing to the fact that the introduction of organometallic reagents decreased the solvent temperature and terminated the particle growth. The subsequent heating of the reaction mixture not only provided control over the particle size, but also ensured the particle annealing; this resulted in ordering of the crystal structure and extrusion of defects from the particle bulk. The particles obtained in this way had a uniform shape and a passivated surface and demonstrated a relatively steep absorption edge and a narrow luminescence spectrum at room temperature.
Later, a new high-temperature colloidal synthesis was used to obtain QDs based on semiconductors of various types: AIIBVI, AIIBV and AIVBIV (see references in Refs[238] and [239]). Thus, the proposed method not only enabled the control of the particle size and particle size distribution, but also provided particles with minimized concentration of defects and a nearly ideal crystal structure. Further development of this method included the search for new precursors, ligands and methods of surface modification in order to enhance the luminescence efficiency.
2.2. Synthesis of QDs in a solid matrix
The knowledge of the synthesis of glasses and glass colouring and properties was summarized by I.I.Kitaigorodsky[240], V.V.Vargin[241] and W.Weyl[242] in the first half of the 20th century. In addition, Weyl was one of the first to observe the Tyndall effect in coloured glasses. The appearance of this effect implied that these glasses were composed of a matrix with dispersed colloidal dye particles. Classical examples of colloidal glass colouring are gold ruby and cadmium glasses. In the former case, colloidal particles of gold metal are formed in glass and colour the glass red. In the latter case, particles of cadmium chalcogenides are grown and cause yellow to red colour of glass.
Currently, glasses are widely used as matrices or substrates because of their inertness. The growth of QDs in an inorganic glass c can result in chemical, thermal and mechanical stability, thus providing a long service life and good prospects for the manufacture of devices[243, 244].
2.2.1. Glass melt quenching
The formation of semiconductor nanoparticles in a glass matrix includes preparation of a supersaturated solution followed by its phase separation[245]. A supersaturated solution is obtained by decomposition of the initial glass components at high temperature and subsequent quenching of this state. The QD formation in an amorphous glass matrix is based on the thermodynamic precipitation from a supersaturated solution (Figure 4). The isolation of a semiconductor phase in a glass matrix is caused by its low solubility at low temperature; it is controlled by ion diffusion and is accomplished via the heat treatment of glass in the glass transition temperature range[244-246]. This system can be conceived as a solution in which the glass matrix is the solvent and the QD-forming ions are the solutes[243, 244, 246]. At high temperature where glass exists as a melt, this solution is not supersaturated. However, as the temperature decreases on cooling of the melt, the solution becomes supersaturated. The glass viscosity at room temperature is too high for the formation of QDs upon ion movement. A sufficient ion diffusion and active ion movement start at the glass transition temperature \( T_g \). The QD growth in glass occurs in three stages[245, 247, 248]. Nucleation takes place in the first stage through random fluctuations of the local concentrations of reactants. The second stage is the diffusion-limited growth of the nuclei in which the average nanoparticle size increases in proportion with the square root of the heat treatment time. When the concentration of available reactants decreases to a critical level, Ostwald ripening, or competitive growth takes place. In this stage, larger particles grow at the expense of smaller ones, with the average QD radius increasing in proportion to the cube root of the heat treatment time[245, 247]. Owing to the difference between the activation energies of the nucleation, normal growth and competitive growth, it is possible to obtain QDs of identical size by appropriate combination of heat treatment temperature and time[246]. In the general case, the longer the heat treatment or the higher the temperature, the larger the QD size. The Gibbs free energy difference is the driving force for the change in the local concentration of the reactants. Thus, the initial state is unstable provided that any vibration can reduce the free energy. Hence, the rate-limiting diffusion process becomes the only obstacle to these fluctuations. The heat treatment in the temperature range \( T_g < T < T_m \) makes it possible to overcome this limitation and attain the final stable state (\( T_g \) is the glass transition temperature at which cleavage and repeated formation of covalent bonds in the amorphous network take place, and Tm is the melting temperature of the matrix at which the glass viscosity is rather high)[246, 247].
After successful synthesis of CuCl, CuBr, CdS and CdSe QDs in glass carried out by Ekimov and co-workers[231, 232, 249], works along this line were actively pursued by other research teams[250-258]. Although they enabled obtaining and studying quantum dots, a considerable drawback of QDs synthesized in glass was the wide dispersion of particle size. A decade after the first synthesis of semiconductor particles in glass, the procedure used by Ekimov and co-workers was modified: the heat treatment was separated into two stages[37]. Subsequently, this approach was actively used to study the influence of heat treatment conditions on the QD-containing glasses[259-262]. The first heat treatment stage was carried out at temperatures well below the glass transition temperature. This provided the formation of nuclei of the future semiconductor phase. The repeated annealing at higher temperatures resulted in the growth of the existing nuclei. Finally, the separation of nucleation and particle growth processes decreased the dispersion of particle size from 15 to 5%.
One more drawback is the use of high temperatures for the synthesis of glass based on silica. This stimulated the search for new compositions that would enable the synthesis to be performed at lower temperatures (below 1673 K, or 1400 ºC): telluride, phosphate, germanate and gallate glasses[263-265]. They are manufactured by replacement of Si by Te, P, Ge and Ga with a minor loss of stability for better transmission at a definite wavelength. However, new materials had poorer mechanical properties than silica-based glasses.
2.2.2. Sol – gel method
The sol – gel method is based on the use of high-purity starting compounds, which are homogeneously mixed in the liquid phase. The chemical hydrolysis and condensation reactions are carried out to give stable transparent sol system in solution (Figure 5a)[266]. Then sol is subjected to ageing to form a three-dimensional network with a non-flowing solvent. After that, the gel is dried and sintered to obtain a material of molecular or even nano-scale structure. After a successful use of the sol–gel process to implant QDs into a transparent silicate glass at relatively low temperaturs[235], this method proved to be reliable and convenient for obtaining QDs in solid matrices[267, 268]. However, it was difficult to obtain bulk samples owing to high residual stresses arising in the silicon-and-oxygen framework after removal of the solvent. Nevertheless, this method allowed obtaining QD-based composites as thin films.
2.2.3. Ion implantation
According to this method, ions accelerated with an electron field are injected on a material surface to form defects or composite structures (Figure 5b)[269]. Initially, this method was used for doping of semiconductors, but it was soon adapted to study the effect of implantation in a silicate matrix[266, 267]. Subsequently, attempts were made to implant various ions into glass to obtain metallic, semiconductor and ferromagnetic nanocrystals[271-274]. Despite the fact that ion implantation method allows for controlled formation of QDs, the penetration of the implanted ions is restricted to the surface layer of the matrix (several hundred nanometres) and barely reaches its interior. This results in increasing size dispersion of QDs and complicates the control of QD distribution across the matrix. In addition, the ion beam may damage the matrix, and the equipment used to implement this method is sophisticated and expensive.
2.2.4. Ion exchange method
One more method that was used for the synthesis of QDs in a solid matrix is ion exchange, which is a chemical reaction on the surface of a solid matrix placed in a salt solution (Figure 5c)[270]. The most reactive monovalent ions, Na+, K+, Ag+ and Cu+, are used for modification of materials[275-277]. Although QD precipitation can be performed in a near-surface region up to 5 mm depth, the exchange area is still too large and cannot be accurate to a micron level in three dimensions[271]. In addition, it was shown that the interaction of a plasmon with an electric field may promote precipitation of QDs and affect the spatial distribution of particles, thus changing the position of photoluminescence bands[278].
2.2.5. Femtosecond laser irradiation
The use of a femtosecond laser was yet another attempt to separate the nucleation and growth processes[279]. The irradiation leads to a local heating of the matrix, which initiates the nucleation of a new phase (Figure 5d). The process is controlled by laser beam parameters such as temperature and time of treatment. The growth of the nuclei takes place during the subsequent heat treatment. This method has been also successfully used in other systems for selective QD growth, including Ag[280], Cu[281], Si[282] and InGaAs[283] nanoparticles. In addition, CdSe[279] and PbS[271] QDs were synthesized in glass using a femtosecond laser and heat treatment; however, long-term laser irradiation resulted in increased size dispersion of particles and damage to the glass matrix.
To date, the fundamental mechanisms of QD nucleation and growth are well-understood and described in the literature[245], but there are still quite a few unsolved challenges. Studies of the kinetics of nucleation and crystal growth are limited, most often, to glass ceramic systems, in which the major glass component crystallizes during heat treatment (see references in Refs[284] and [285]), but little is known about the nucleation and growth of the particles of minor components or trace elements in glass. Therefore, the subsequent studies addressed the mechanisms of growth of QDs embedde into an amorphous matrix and to their atomic structures and optical properties (see Chapter 3)[261, 286-293].
2.3. Synthesis of QDs in colloidal solutions
2.3.1. Nonaqueous synthesis of QDs
The results obtained in the early 1980s gave an impetus to the synthesis and study of colloidal QDs. The main goal was to obtain monodisperse particles with an ideal crystal structure and intense luminescence. It was found that defects on the QD surface and poor surface passivation were the main causes for the low efficiency of luminescence. This discovery stimulated several research groups to develop effective methods for improving surface quality and passivation. At the end of 1980s, CdSe clusters were synthesized from organometallic precursors by the reverse micelle method, and the cluster surface was chemically modified[49]. The application of organoselenides (e.g., PhSeSiMe3) influenced the kinetics of particle formation and growth, and also stabilized and passivated the surface via the formation of covalent bonds between the surface cadmium atom and the ligand selenium atoms. The opened possibility of obtaining stable non-agglomerated particles gave rise to ideas concerning the synthesis of complex core/shell structures. The first successful approaches were based on surface passivation by depositing an inorganic shell consisting of a semiconducting material with a wider band gap compared to that of the core material[87, 114, 294]. It was demonstrated in relation to CdSe QDs that their coating with a ZnS shell leads to the surface passivation and considerably increases the luminescence efficiency in the core[114].
The use of coordinating solvents (e.g., pyridines or phosphines) was the next step in the development of methods for the synthesis of colloidal QDs (Figure 6). In particular, phosphines can coordinate both metal and chalcogen atoms. High-quality crystalline CdS QDs were obtained by the reaction of organometallic precursors in tri-n-bitylphosphine oxide in an Ar atmosphere at temperatures above 473 K (200 °C)[228, 295]. Having continued the experiments using coordination solvents and high temperatures, Murray, Norris and Bawendi reported a successful synthesis of monodisperse crystalline CdS, CdSe and CdTe QDs[51]. Three years later, Hines and Guyot – Sionnest[87] corrected the procedure (reactant concentrations and solvent temperature) and synthesized stable CdSe/ZnS core/shell colloidal QDs with a narrow size distribution and a high degree of crystallinity and luminescence efficiency. The average diameter of the CdSe core and thickness of the ZnS shell were 2.8 and 0.6 nm, respectively. Owing to efficient surface passivation, the luminescence quantum yield reached 50% at room temperature. Chemseddine and Weller[296], who worked independently of Bawendi’s research team, synthesized CdS QDs in dimethylformamide using thioglycerol as a stabilizer and performed chemical separation of the particles on the basis of their size-dependent solubility. The proposed procedure allowed scaling-up of QD synthesis up to a few grams. Yet another step towards increasing the volume of the obtained material, while maintaining control over the particle formation and growth and, consequently, characteristics of the material, is the so-called heat-up or thermal ramp method. Unlike the method proposed by Bawendi, the new process was not based on fast changes in temperature upon the addition of one of the precursors. Instead, the temperature gradient was used. The selection of temperature-sensitive precursors and heating conditions made it possible to separate the particle nucleation and the subsequent particle growth in time (see review [297]).
After the discovery of high-temperature synthesis, studies of QDs were developed along several directions. An important step was made by switching from toxic, self-flammable Cd(CH3)2 precursors unstable in air and at room temperature to less harmful compounds [CdO, CdOC(O)CH3][298]. Today, more complex core/shell QDs have been obtained, non-radiative Auger processes have been suppressed, the degree of crystallinity of the shell has been increased and the surface has been passivated with various ligands; this expanded the scope of biomedical applications of QDs (see references in Refs[299-301]). In addition, more complex heterostructures such as dots-in-rods were fabricated[302]. New heterostructures are promising for the use in display technologies and other optical applications due to the following properties: they exhibit polarized luminescence with high quantum yield and also demonstrate the possibility of luminescence switching under the action of an electric field. Ithurria et al.[303, 304] synthesized new quasi-2D nanoplatelets with a thickness of one to a few monolayers and electronic properties similar to those of quantum dots. The increase in exciton binding energy and the giant oscillator strength make 2D platelets especially fast luminophores. The development of a strategy for the synthesis of two-dimensional structures resulted in the preparation of 2.5 to 5 monolayer thick CdSe nanoscrolls[305-307]. The unique two-dimensional rolled structures exhibited a pronounced circular dichroism upon hybridization with chiral molecules; therefore, these systems are of interest for optoelectronic applications using polarization effects. Having experimentally disproved the assumption that QDs are capable of spontaneous self-cleaning from crystal lattice defects, Norris et al.[298] and Schimpf et al.[308] demonstrated successful targeted doping of QDs. The use of cation exchange as a post-synthetic modification of nanostructures allowed for step-by-step fabrication of complex nanomaterials and precise control of their chemical and phase composition[309].
Despite all benefits of QDs obtained in this way, the synthesis in organic nonpolar solvents restricted the QD solubility in water; this became a key issue for the development of methods for the transfer of high-quality hydrophobic QDs into aqueous solutions for the subsequent bioconjugation (see reviews[134, 310-313]). The main strategies for QD solubilization can be subdivided into three groups. The first approach is based on ligand exchange and the use of bifunctional compounds capable of replacing organic solvent molecules on the QD surface. These compounds contain hydrophilic groups (e.g., –NH2, –COOH), which turn out to point into the solvent after being attached to the QD surface, thus providing water solubility. The second approach consists in the formation of a polymer layer around QDs via penetration of hydrophobic moieties of the already present ligands into the new organic shell. The third strategy implies encapsulation of QDs into polymer microspheres or microcapsules. As other achievements in biomedical applications, note the fabrication of conjugates with peptides, proteins and DNA, development of biological and diagnostic tests and the creation of multi-colour fluorescent labels for ultrasensitive detection and imaging. Despite the attained progress and active development of this field, a number of problems remain unsolved in QD bioadaptation: it is necessary to attain reproducibility of transfer to the aqueous phase and surface functionalization and to develop non-destructive methods of QD conjugation with biological molecules.
Thus, thousands of scientists and engineers now use high-temperature synthesis and its varieties. The procedure proposed by Murray, Norris and Bawendi has become a versatile and reproducible chemical strategy for the synthesis of monodisperse QDs over a broad range of sizes. Unlike QDs in a glass matrix, liquid colloidal systems can be used for QD growth, surface passivation, substitution of solvent and ligand molecules and for the fabrication of multilayer structures by spin-coating.
2.3.2. Aqueous synthesis of QDs
Apart from the development of methods for QD synthesis using organometallic precursors and organic solvents, works on the QD synthesis in aqueous solutions was also continued. The advantages of aqueous synthesis are environmental friendliness, solvent biocompatibility and stability in air, scalability of the synthesis and wide possibilities of QD functionalization. The method is based on the exchange reaction with precipitation from aqueous solutions. The QD synthesis by chemical precipitation requires the presence of three components: a source of the metal, a source of the chalcogen (chalcogenizer) and a stabilizer. As sources of metal ions, water-soluble salts are used. Sodium sulfide has been used to introduce sulfur ions into the system[314]. The replacement of sodium sulfide with thioacetamide[314] or thiourea[315] made it possible to control the sulfur release and thus to control the rate of sulfide formation. The H2Se and H2Te gases formed upon decomposition of the corresponding aluminium chalcogenide serve as sources of selenium and tellurium[231, 316, 317]. Other suitable reagents are solutions of NaHSe[318] and NaHTe[319], which are prepared by the reduction of elemental Se or Te in a NaBH4 solution. In addition, electrochemical generation of H2Te for QD synthesis was developed[320, 321].
The use of stabilizers makes it possible to control nucleation in early stages and to restrict the particle growth. By choosing appropriate stabilizers, it was possible to extend the range of QDs obtained in water from CdS to ZnS[322], ZnSe[231], PbS[323], CdTe[313], Cd3P2[324], etc. The shell formed by the stabilizer not only provides solubility of QDs in water and prevents agglomeration, but also acts as a structure through which QDs interact with the environment. Maleic acid and styrene copolymer, phosphates and polyphosphates were the first compounds to be used as stabilizers. In later studies, chelating peptides, thiols, amines, biomolecules (bovine serum albumin, DNA, RNA) and other compounds were used[5, 313, 325-328]. Among the stabilizing agents, thiol-containing ligands are compounds of choice, because they are effective for the formation of monodisperse QDs of a wide range of semiconductor compounds containing cadmium, zinc, lead, silver, copper and mercury ions[316-319, 329-333]. Owing to the use of various short thiols as stabilizing ligands, aqueous synthesis can be considered as an alternative to QD preparation in high-boiling solvents. Quantum dots obtained in this way showed very efficient luminescence (40 – 60%). The use of thiol-containing stabilizers makes it possible to control the kinetics of QD synthesis, passivates the surface and provides the stability, solubility and surface functionalization of nanoparticles.
The attempts to reach the smallest possible particle size and the maximum possible monodispersity of QDs resulted in the creation of ultrasmall molecule-like monodisperse (100%) semiconductor clusters with a definite size, structure and characteristic optical properties[334-336]. The cluster synthesis proved to be an exception to common practice: as a rule, QD synthesis in an aqueous medium does not give particles with a monodisperse size distribution. Therefore, a procedure for size-selective precipitation has been developed, first applied to CdS QDs (Ref. [296]) and is widely used for both organometallic and aqueous synthesis.
The low synthesis temperatures in aqueous solutions hampered the preparation of particles with an ideal atomic structure. Subsequently, microwave irradiation and autoclave synthesis were used to improve the QD crystallinity, size distribution and optical properties. The proposed modifications of aqueous synthesis made it possible to obtain not only doped QDs but also core/shell and core/shell/shell QDs (see references in reviews[47, 337]). The preparation of such intricate structures directly in water has become an important step towards high-quality QDs, which were previously accessible only via organometallic synthesis.
Over the past two decades, a substantial progress has been made in the preparation and study of water-soluble QDs, the luminescence of which covers a wide spectral range depending on the material and the particle size. Among benefits of aqueous synthesis, note its simplicity, high reproducibility and the possibility of scaling up for commercial QD production. In addition, the obtained QDs can be purified, precipitated and stored as a powder under ambient conditions for many years, with the particles remaining stable and readily soluble in water.
Thus, the crucial role in the formation of QD properties is played by the method of their synthesis. The synthesis in a solid dielectric or polymer matrix may produce nano-sized particles isolated from one another by the matrix material, which, under certain conditions, preserves the unique semiconductor and optical properties of nanoparticles and prevents them from agglomeration and undesirable interactions. One more benefit of QDs in a solid matrix is the possibility to subject the samples to additional mechanical and chemical treatment without deteriorating the functional properties of materials. Meanwhile, advantages of QD formation as a colloidal system include the possibility of three-dimensional interaction of the QDs with their environment, i.e., a larger accessible surface area and contact with the surrounding medium. Therefore, they can be used, for example, as DNA labels or to monitor biological and chemical changes in a particular environment. A colloidal system also provides the possibility of replacing the solvent surrounding quantum dots, depositing QDs on a substrate or replacing the liquid medium by a polymer. This flexibility makes mass production of QDs promising.
3. Optical properties of colloidal quantum dots
3.1. Quantum size effect in optical absorption
A basic feature of the energy structure of the semiconductor colloidal QDs is the discrete energy spectrum (size quantization). The size quantization effect is manifested as a blue shift of the optical absorption spectrum following a decrease in the particle linear size to a few nanometres (see Figure 2)[24, 25].
Due to the possibility of attaining high optical uniformity of semiconductor QD samples in glasses and colloidal solutions, discovered back in the first experiments, optical absorption spectroscopy has become the analytical method most actively used to study the quantum size effect[29, 30, 32, 43-46]. The appearance and size dependence of a structure in the optical absorption spectrum of QDs (Figure 7) was accounted for by the discrete system of energy levels[31, 338]. Therefore, in the case of QDs, the quantum size effect became a unique tool for the control of the optical absorption and luminescence region from the IR to UV range by changing only the size of nanocrystals.
The discrete structure of the energy states and optical absorption spectra of semiconductor QDs is of crucial importance and fundamentally distinguishes QDs from plasmonic nanoparticles, for which \( E_{i+1} – E_i \ll kT \), and the optical resonances are associated with the appearance of localized plasmons upon the interaction of light with collective vibrations of electron gas confined by the nanoparticle walls[339].
The principles of interpretation of the optical absorption spectra were formed almost simultaneously with the fabrication of the first QD samples in glasses and colloidal solutions and with experimental observation of the blue shift of the absorption spectra with decreasing QD size (quantum-size effect) and were always based on the model views on the energy structure of the quantum system. The first rigorous analytical consideration of the quantum mechanical problem for an electron (hole) and the Wannier–Mott exciton in a spherically symmetric potential well with infinitely high walls was performed by Soviet physicists Alexander and Alexey Efroses[31]. This elementary theory describing the size quantization effect in QDs is developed in terms of the effective mass method and is actually a zero approximation of the \( k \cdot p \) theory developed later.
In the simplest case of severe confinement, i.e., when the Coulomb interaction between an electron and a hole in QD with a size smaller than the Wannier – Mott radius in the substance is neglected, the theory demonstrates size quantization of the energy states of electrons (holes) \( E_{n,l}^{e(h)} \) for which quantum numbers \( n \) and \( l \) have a meaning similar to that of the quantum numbers in the hydrogen atom problem. It was shown that the allowed level with the minimum energy (s states, \( l = 0 \)) for electrons (holes) is determined by their kinetic energy as \( \frac{\hbar^2 \pi^2}{2 m_{e(h)}^* R^2} \)
where \( \hbar \) is the Planck’s constant, \( m_{e(h)}^* \) is the effective electron (hole) mass, \( R \) is the radius of the spherical nanocrystal. The quantization of energy levels for a particle of radius \( R \) in an analytical form for s-states results in increasing gap between the size-quantized states occupied with electrons and completely vacant conduction states
where \( E_g^{eff} \) is the effective band gap of QDs, \( E_g \) is the band gap of the bulk crystal, and \( \mu=\frac{m_e^* m_h^*}{m_e^*+m_h^*} \)
is the is the reduced effective mass for the corresponding crystal. The \( E_g^{eff} – E_g \) is called, in some cases, retention energy. This value decreases with increasing QD size and disappears when the requirements for the existence of quantum size effect are no longer met.
An important result of this consideration is the discrete structure of the optical absorption spectra differing from that for the bulk semiconductor and representing a system of discrete lines. The allowed optical transitions are those between the levels with equal quantum numbers[31].
where \( \alpha \) is the absorption coefficient, \( E_{ph} \) is the energy of an incident photon existing under the same conditions (temperature, pressure) as the QD being studied, and \( k_{n,l} \) is the set of values of the wave vector determined by zeros of the Bessel function with the half-integer \( J_{l + 1/2}(k_{n,l}, R) = 0 \) and for s-states equal to \( k_{n,0}R = \pi n \). In essence, the invariability of the wave vector for the allowed optical transitions in QDs is similar to the case of vertical (direct) transitions in the bulk semiconductor crystals.
In this description, the energy of the longest-wavelength optical absorption transition depends on the nanocrystal size and corresponds to \( n=1 \).
Thus, the elementary theory provides an explanation to the size quantization effect in QDs and to the dependence of the optical absorption energy on the QD size and an estimate of the energy of higher-energy transitions. One more benift of this elementary formalism is clear demonstration of the size effect in the experimentally observed absorption spectra of QDs. Correspondingly, processing of an experimental optical absorption spectrum implies determination of the position of the most probable transition rather than approximation of the spectral edge by an appropriate power function. However, the real situation is such that no combination of materials can reproduce the ideal case of a well with infinitely high potential walls. The use of this model is justified only for an approximate estimation of the size quantization effect for the quantum states located most closely to the effective band gap in the energy spectrum[54, 236]. Taking into account the finite height of the potential barrier for the carriers at the QD boundary leads to decreasing effective band gap and red shift of the optical absorption spectra[55, 66, 67].
Simultaneously with the development of the first original protocols of colloidal synthesis in polar solvents, a significant discrepancy was found between the empirical size dependence of the long-wavelength optical transition energy and that calculated in the strong confinement approximation[31], especially in the region of small QD sizes. This led to the need to consider optical transitions with allowance for the exciton formation. A specific feature of an exciton in QDs of a few nanometres in size, i.e., comparable with the radius of the Wannier–Mott exciton in the corresponding substance, is its predominant spatial localization within the nanocrystal, that is, confinement and increase in the Coulomb interaction in the non-equilibrium state that retains this elementary excitation up to annihilation. This is the basic distinction of QD from quantum wire or quantum well and also from a bulk crystal that has at least one or two coordinates along which charge carriers have no confinement and may happen to be located at distances much longer than the radius of the Wannier–Mott exciton.
Brus and co-workers[43-46] specified expression (2) in the framework of the effective mass method, taking into account the Coulomb interaction between an electron and a hole.
In the case of small-size QDs, the \( E_g^{eff} – E_g \) value considerably exceeds the exciton binding energy in the corresponding single crystal, while the effective exciton radius is determined, first of all, by the confinement at the crystal interfaces. Therefore, the Coulomb interaction is treated as a first-order correction in the framework of perturbation theory.
Kayanuma[52] additionally took into account the spatial correlation of an electron and a hole and modified the Brus formula.
where \( E_{Ry}^* \) is the Rydberg energy.
This elementary approach provides a qualitative explanation for the blue shift of the absorption edge with decreasing size of nanocrystals, but does not allow interpretation of the whole absorption band structure.
The development of chemical processes for the preparation of colloidal QDs of various compositions and sizes using various matrices and various passivating agents brought about the need for unambiguous interpretation of their optical absorption spectra. The development of the relevant principles required modelling of the QD energy structure and the system of optical transitions that form the absorption band, transition cross-sections and so on. This fundamental spectroscopic problem is tackled in quite a number of studies, the history of which includes hundreds of studies published since the discovery of QDs until now (e.g.[329, 334, 340-368]). These studies are traditionally developed using two approaches. The first approach is semiempirical, vivid and adheres to the \( k \cdot p \) theory in the effective mass approximation[52-72]. The second approach is atomistic and implies ab initio calculations and consideration of the nanoparticle structure at the atomic level using the tight binding, pseudopotential and density functional theory methods[73-86].
Numerous experimental spectroscopic studies of colloidal QDs showed that real optical absorption spectra do not have a discrete structure, which is predicted by elementary model views[31, 55, 43-46]. Most often, optical absorption spectrum of colloidal QDs is a broad complex band, the structure of which cannot be detailed according to the Rayleigh criterion for spectral resolution. In some situations, the observed spectra exhibit no characteristic structure corresponding to exciton transition peaks[72, 110, 338, 368, 104-106].
The construction of a theoretical model of optical absorption adequate to the experimental results required consideration of the complex structure of the valence band states, including the appearance of heavy, light and split-off hole subbands and effects caused by band non-parabolicity effects[338, 68-72]. One of the first successful attempts of relatively full interpretation of the optical absorption spectra, taking into account the diversity of optical transitions, was performed for colloidal ZnSe, CdSe and InP QDs[69, 338, 369].However, in this case, too, the applicability of the band concept to small-size nanocrystals remained an open question. The positive answer to this question was given by atomistic calculations of the QD energy structure. These calculations were activated gradually, in parallel with the progress in the computational power. Calculations were initially performed for clusters consisting of a few tens of atoms and then for nanocrystals of approximately 1 – 1.5 nm size; currently, it is possible to calculate the energy structure of 2 – 5 nm QDs taking into accounts atoms (molecules) of the environment[73-75]. Ab initio calculations give a full amount of information such that it is often difficult to distinguish contributions of different physical factors in the obtained results. Furthermore, these calculations have not yet been performed for all widespread nanocrystal compositions. Characteristic examples are non-stoichiometric compounds of silver sulfide and selenide and other.
An important result of ab initio calculations for QD energy structure is the proof of discrete structure of the energy spectrum for electrons and holes[78], similar to that obtained using the effective mass approximation[31]. Thus, an important stage in interpretation of the results is comparison of the data obtained by the \( k \cdot p \) theory and atomistic calculations.
Many-year research[69, 338] resulted in the appearance of a definite spectral nomenclature, representing sequences of optical transitions. As an example, Figure 7b (upper continuous curve) shows interpretation of the spectrum of finely dispersed CdSe QDs, with allowance for the results of calculation performed in the cited studies using the \( k \cdot p \) theory (lower dashed curve), while Figure 7a shows the data for less finely dispersed CdS QDs with allowance for the complex structure of the valence band and band non-parabolicity[72, 338]. These studies consider not only the transition energies between the heavy, light and split off hole and electron bands, but also their relative intensities. However, the transition sequences for exciton absorption may differ for QDs of different semiconductor compounds. For example, the system of transitions for CdSe QDs starting from the lowest energy has the form: 1S3/2 – 1Se, (1P3/2 – 1Se is forbidden and does not contribute to absorption), 2S3/2 – 1Se, 1P3/2 – 1Pe (according to other data[94, 338], 1S1/2 – 1Se) and so on. In the case of InP QDs:[370] 1P3/2 – 1Se (forbidden and does not contribute to absorption; however, this minimum-energy transition determines the luminescence peak and the dynamics of exciton decay), 1S3/2 – 1Se, 1S1/2 – 1Se, etc. The sequence of transitions for CdS QDs is also determined by the crystal structure. When CdS QDs crystallize in the wurtzite system, the sequence of transitions is similar to that for CdSe QDs[370]. For crystallization in the sphalerite type, the \( k \cdot p \) theory indicates that the lowest-energy absorption is forbidden for small CdS QDs, since the ground state of the electron envelope wave function has s-symmetry and hole envelope wave function has p-symmetry[68, 371, 372]. The next absorption transition involves s-symmetric hole envelope wave functions and is allowed. This theoretical result was experimentally confirmed in a study of low-temperature luminescence[373]. In the case of large CdS QDs, the order of s- and p-type levels of holes changes, and the lowest-energy transition becomes allowed. The relative contributions of not only allowed but also forbidden transitions to the optical absorption spectrum may markedly change, for example, due to SD mixing effect[4]. For example, transitions involving the 1S-electron state are possible from not only 1S3/2 and 1S1/2 hole states, but also from other S-states. Owing to the SD-mixing, the transitions to the D-electron level are possible from both S- and SD-states. Thus, a universal nomenclature of optical transitions determining the absorption spectra has not yet been formed. In each case, full calculation of the energy structure of QDs is required, at least in terms of the \( k \cdot p \) theory.
Apart from the influence of the complex energy structure of the valence band, one more cause for the homogeneous broadening of real optical absorption spectra of QDs is the electron – phonon coupling. The homogeneous broadening problem was first addressed apparently by Bawendi et al[368]. The recording of optical absorption spectra of CdSe QDs samples with a size dispersion of 8% at temperatures of 5 – 15 K showed a considerable contribution of the electron – phonon coupling to spectrum broadening. The use of low-temperature luminescence excitation spectra, reflecting the absorption of luminescent monodisperse QDs, contained a number of discrete electron transitions and longitudinal optical (LO) phonon progressions[368].
Numerous experimental studies of the optical properties of colloidal QDs demonstrated that the inhomogeneous broadening has a predominant influence on the structure blurring in the absorption spectrum[72, 94, 104, 105, 338, 374]. The main cause is size dispersion of QDs in an ensemble. Figure 7 a shows the transformation of the absorption spectrum structure in the case of broad size distribution of CdSe QDs. Also, Figure 8 shows a comparison of the optical absorption spectra of three colloidal Ag2S QD samples passivated with thioglycolic acid, with the size dispersions of two samples differing by a factor of more than two (cf. 1 and 3)[375].
The inhomogeneous broadening of the absorption spectra of Ag2S QDs may be due to one more reason, thst is non-stoichiometry of QDs related to both the variability of defect concentration within a single nanocrystal and the quality of passivation of their interfaces (the interfacial states are QD dangling bonds). In the latter case, spectral edge is smeared because of an additional contribution of impurity absorption (Figure 8, curve 2). Hence, determination of the size effect in the optical absorption by approximation of the long-wavelength spectral edge is not quite correct. The exciton absorption transition energy should be determined from the peaks present in the spectrum. If there are no clear-cut peaks, the position of the minimum of the second derivative of the optical density spectrum with respect to the emission quantum energy is determined. This technique was proposed in early studies devoted to the spectroscopy of the QD size effect[35, 338] and is used until now[110, 104-106, 376-378]. It was shown that the accuracy of determination of the position of the irregularity (inflection) observed at the long-wavelength edge of the structureless QD absorption spectrum due to the exciton transition to the ground state from the minimum of the second derivative gives an error not exceeding 0.02 eV.
Thus, studies of the quantum size effect in the optical properties of QDs indicated the necessity to take into account the effects of homogeneous and inhomogeneous broadening, with interpretation of optical absorption spectra being unambiguous. An important stage is also to compare the obtained spectral behaviour with the results of structural studies, in particular with the average QD size determined by TEM and/ or from broadening of X-ray diffraction peaks.
The possibility of predicting the optical properties of QDs for subsequent various applications is provided by the empirical size dependences of exciton absorption transition energy in comparison with analogous dependences obtained most often using Brus (5) and Kayanuma (6) relations.
From the spectroscopic standpoint, the size dependence of the exciton transition energy is valuable also due to the fact that it can be used to relate the size dispersion to the half-width of the absorption (and luminescence) bands
where \( H \) is the half-width of the spectral absorption (or luminescence) band caused by the size distribution of nanocrystals in the ensemble \( \Delta r \), and \( \frac{d E_g^{eff}}{d r} \) is the derivative of the exciton transition energy with respect to the nanocrystal size.
Figure 9 shows the size dependences of the energy of the ground exciton absorption transition for different QDs (CdS, Ag2S, CdSe, PbS) that we obtained using the results of published papers (Refs [51, 52, 78, 103, 126, 132, 141, 145, 150, 329, 334, 379, 340-348, 350-367]). First of all, attention is attracted by the fact that the experimental size dependence of the ground exciton absorption transition energy is only in qualitative agreement with this dependence found by calculations using the \( k \cdot p \) theory. In some cases, the empirical size dependences are close to those calculated by the Kayanuma formula (Figure 9, blue dot-and-dash curve)[52]. In other cases, a considerable deviation is observed, especially for small-size QDs. This situation is clearly seen for CdSe QDs. Meanwhile, the calculation of the energy structure using the pseudopotential method[78] gives a size dependence for these QDs similar to the empirical one (see Figure 9, red crosses).
Figure 9 demonstrates that the success in the study of the size dependence of the absorption behaviour is rather modest for semiconductor QDs with a complex crystal structure. Silver sulfide tends to form non-stoichiometric nano-sized crystals Ag2±δS with noticeable cobncentration of defects, giving rise to a system of localized states with different activation energies[375, 380-387]. Consequently, the available experimental data on the quantum size effect in the absorption properties of QDs are contradictory. In some studies, relatively large particles (a few nanometres) have an absorption edge in the visible region[353, 383, 388-391]. However, for Ag2S nanocrystals of 4 – 5 nm or more in size, the absorption edge virtually does not undergo a blue shift[145, 352, 392-395]. A pronounced size effect with a shift of the absorption spectrum to the visible region is observed when the QD diameter is reduced to 1 – 2 nm[104, 106, 352]. At the same time, the absorption edge located in the IR region was found for Ag2S nanocrystals[353, 388, 391].
Apart from the dependences shown in Figure 9, fairly convenient empirical expressions for size calculation from the energy or wavelength of the exciton absorption peak are often used. These expressions are obtained for QDs of various compositions by approximating the size dependence by a polynomial, power or hyperbolic function as experimental methods for the preparation of monodisperse QDs of various semiconductors are being advanced, the experimental data on the size dependence of exciton absorption peak are being accumulated and analytical methods for determination of the average size of QDs are being developed.
For example, relying on the large set of experimental data on the sizes for a series of colloidal CdS, CdTe and CdSe QDs, determined by transmission electron microscopy and optical absorption spectroscopy, Yu et al.[348] derived expressions for calculating the size of spherical CdTe, CdSe and CdS QDs from the known exciton absorption peak energy.
where \( d \) is the QD diameter (nm), \( \lambda \) is the long-wavelength absorption maximum.
Lin et al.[352] proposed an empirical formula for Ag2S QDs describing the dependence of the exciton transition energy on the size measured by TEM
In the limiting case of bulk crystal (\( d \rightarrow \infty \)), this expression gives the exciton binding energy (0.096 eV), which is consistent with the value calculated by the effective mass approximation (0.104 eV).
It is noteworthy that a variety of different empirical formulae are available from the literature for QDs of the same composition. Figure 9 depicts these size dependences derived from empirical formulae (10), (11), (12) for PbS QDs. Formula (10) was proposed by Cademartiri et al.[365] (see Figure 9, light-blue curve).
where \( R \) is the radius of a spherical nanocrystal.
Moreels et al.[367] reported a somewhat different dependence (see Figure 9, brown curve).
The two above dependences proved to be similar, whereas expression
reported by Weidman et al.[366] (see Figure 9, black curve) is markedly different from (10) or (11).
A similar situation was found for Ag2Se QDs. Relying on the size dependence of the exciton transition energy reported by Sahu et al.[396] for QDs with diameters of 6 nm or less with a tetragonal crystal lattice, the following expression was obtained:
where \( R \) is the QD radius in nm. Langevin et al.[397] proposed a different expression for orthorhombic Ag2Se QDs.
where 1.056 eV is the limit to which the empirical curve tends with increasing size. This should correspond to the absorption edge of bulk Ag2Se. In the authors’ opinion, the deviation from the known band gap of this compound equal to 0.15 eV for the orthorhombic lattice[398] is mainly due to the high excited states of the exciton rather than to the ground state.
It is noteworthy that, in addition to the size dependences of the exciton transition energy in the optical absorption of colloidal QDs, attempts were made to find the size dependences of molar extinction coefficients[334, 348, 367, 399]. However, these dependences are different for QDs of different compositions. In the case of CdS, CdSe, CdTe, PbS and PbSe QDs, a super-quadratic increase in the molar extinction coefficient with increasing QD size is observed most often[348]. The absolute values of this coefficient do not exceed 106 L mol cm–1. The exciton absorption intensity depends on many factors and, therefore, it is practically convenient to use the molar extinction coefficient for the short-wavelength part of the absorption spectrum, corresponding to high excited exciton states, to find the QD concentration in a colloidal solution[367].
3.2. Quantum size effect in luminescence
Historically, for ensembles of semiconductor colloidal QDs, the size effect in the optical absorption and photoluminescence spectra was discovered almost simultaneously[34, 41, 42, 338]. The photoluminescence of colloidal semiconductor QDs also features size-dependent parameters of the corresponding spectral bands (e.g., [132, 138, 348, 392]). However, due to the strong dependence of photoluminescent properties on the chosen procedure of QD synthesis and on the electronic structure of the semiconductor used to prepare QDs[100, 399], the size effect in luminescence is much more complex than that in optical absorption spectra. Photoluminescence is only one of the channels for the decay of electronic excitations formed as excitons upon the optical absorption of light by QDs.
Numerous studies of the size effect in the luminescence properties of colloidal QDs have shown that they cannot be interpreted using highly simplified views on the energy structure, similarly to the case of a polyatomic molecule.
Some of the first experimental studies of the luminescence of cadmium selenide and sulfide QDs synthesized in glasses[338] and in aqueous colloidal solutions[42] demonstrated size-dependent exciton luminescence. In other studies, broad luminescence bands with a large Stokes shift were observed for CdS nanocrystals in aqueous solutions[41] and in glasses[100]. Later, using high-temperature synthesis of highly dispersed ensembles of AIIBVI QDs passivated by hydrophobic molecules of TOPO and its analogues[51], narrow (half-width of approximately 10 – 15 nm) exciton luminescence bands with small Stokes shifts were attained; positions of the bands depended on the nanocrystal size in virtually the same way as for optical absorption spectra. Initially, the luminescence quantum yield of such QDs was about 10%. High-temperature synthesis conditions markedly decreased the intensity of the luminescence component caused by recombination at defect levels. The intensity was reduced even further by optimizing the organic complexing agent used for passivation. However, it is also undeniable that the QD luminescence quantum yield is usually noticeably below 100%, irrespective of the luminescence nature. Thus, the need to include QD states caused by non-stoichiometry-induced defects and interfacial states into the energy diagram appeared and disappeared now and then as QD synthesis processes were developed.
It should be reminded that long before the development of QD optics, F.F.Volkenshtein, V.L.Bonch – Bruevich, L.D.Levine, P.Mark, A.N.Latyshev, M.I.Molotskii, R.C.Baetzold and other researchers[400-406] showed that crystal surface defects (adatoms, clusters, crystal surface complexes of organic molecules and ions) form a system of localized states in their band gaps. Calculations of the energies of such states, including analytical ones, which were performed using semi-empirical formulae, showed that they are located within the semiconductor band gaps.
Much later, atomistic calculations confirmed this fundamental result for colloidal QDs. Dangling bonds at the QD interfaces ensure the formation of an additional set of energy levels within the effective band gap, that is, localized states[407-409]. In relation to PbSe QDs, it was shown that non-stoichiometry gives rise to electron and hole trap states with various energy depths[410]. The formation of pseudo-trap states located within the size quantization states filled with electrons, as well as conduction states was found[86]. This problem was analyzed in detail mainly for CdSe, CdS and PbS QDs.
To date, ab initio calculations enabled determination of the role of various effects at the matrix (passivating agent) – QD interface, including structural impurity defects (adatoms, their complexes with organic molecules, vacancies, interstitial ions, etc.), in the formation of the QD energy structure[79, 81-86]. The formation of trap states within the effective band gap associated with the levels of structural impurity defects, which play a significant role in the photophysics of colloidal QDs, was demonstrated[79, 84-86]. The formation of shallow traps below the lowest electronic conduction state, taking into account Cd2+ dangling bonds in CdS, was shown to induce optical absorption on the long-wavelength side (up to several tenths of eV) relative to the energy of the main exciton transition for QDs of the corresponding size[80]. Taking account of S2–dangling bonds yields several types of states with an energy of approximately 0.5 eV above the quantum size state of the valence band[80].
A notable phenomenon is also the formation of localized states of various depths upon passivation of QDs by organic molecules, for example, methylamine or trimethylphosphine oxide, the use of which leads to the appearance of bright exciton luminescence[81]. An important issue for experimenters is to demonstrate the formation of interfacial localized states with an excess concentration of intrinsic and impurity atoms and atom dimers: Se – Se and Cd – Cd dimers on CdSe QD, Pb – Pb dimers on PbS QD, etc[84, 86]. The Cd – Cd and Se – Se dimers at the CdSe QD interfaces and the accompanying traps are unstable. The dynamics of their appearance and disappearance is often limited to a picosecond time scale[84, 411]. The QD photoexcitation may lead to the rearrangement of atoms on the surface and the formation of traps within the effective band gap. It was also shown that non-radiative recombination on the traps associated with cadmium dimers at CdSe QD interfaces occurs much faster than radiative recombination, which indicates that such atomic molecular clusters can act as luminescence quenching centres.
Due to the low concentration of localized states compared to that of size quantization states and lower oscillator strengths of impurity optical absorption transitions, the largest contribution from localized states is present in the photoluminescence of colloidal QDs. Even the first experiments showed that realistic models of QD luminescence require taking into account the effects of photoprocesses involving trap levels at the matrix (passivating agent) – QD interface, including structural impurity defects.100 In turn, these concepts are important for the development of ways to control luminescence parameters (radiative transition energy, luminescence quantum yield, luminescence lifetime, luminescence spectrum half-width) for specific applied tasks.
Now we consider three main modes of luminescence for colloidal QDs, which by now have been established experimentally.
The first mode is direct radiative annihilation of an exciton, the lifetime and probability of annihilation being determined by the quantum confinement of charge carriers that constitute the exciton. Exciton luminescence is characterized by a Stokes shift that does not exceed the exciton binding energy in the corresponding material and by lifetimes of 10 ns to 2 μs[51, 150]. This mode is implemented in nanocrystals, the lattice of which is characterized by perfection and a low concentration of structural defects as well as appropriately chosen passivating molecules at interfaces. A successful choice of the passivating agent ensures a low concentration of dangling bonds, which act as centres of non-radiative recombination[51].
The second mode is the intracentre luminescence observed in QDs doped, for example, with rare earth ions. In this case, the emission occurs as a result of optical transitions between the impurity ion states; that is, it occurs within a centre[412]. This type of emission often features narrow emission lines inherent in certain impurity ions and noticeable (micro- and millisecond) lifetimes of luminescence.
The third mode, recombination or trap QD luminescence, is distinguished by a noticeable Stokes shift exceeding 0.2 eV and a significant half-width of the emission band[413-422]. This luminescence arises at the levels of structural impurity defects formed both inside the QDs[423, 424] and at their interfaces (trap state luminescence) or radiative annihilation of a localized exciton. According to the terminology used in the theory of luminescence of ionic and ionic-covalent crystals, this luminescence in the general case should be classified as recombination luminescence.
The size effect behaves in different ways in each of the QD luminescence modes and is not always similar to the size effect observed in optical absorption spectra.105 Below we consider in more detail the current views on the conditions for emergence and spectral manifestations of the quantum size effect in QD luminescence.
The available data indicate that by changing the parameters of colloidal synthesis it is possible to obtain QDs of various diameters, shapes, and size distributions and thus to control their optical properties[51]. The QDs with exciton luminescence can be prepared in the simplest way by colloidal organometallic synthesis in high-boiling solvents. In this case, they exhibit narrow and intense (with a quantum yield of ≈ 70 – 80%) peaks of exciton luminescence, the parameters of which are fairly stable and strongly depend on the QD size. For a significant proportion of QD compositions with such luminescent properties, there are methods for nanocrystal synthesis and passivation that ensure the suppression of trap recombination luminescence that arises at the levels of structural impurity defects. Controlling the ratio of the components of exciton and recombination luminescence turns out to be a challenging engineering problem that is nevertheless solved. In particular, the influence of non-radiative decay channels of electronic excitation on the luminescence quantum yield can be significantly reduced and the stability of the luminescent properties of QDs can be enhanced by using a semiconductor shell at the final stage of synthesis, with the semiconductor band gap being larger than that of the nanocrystalline core, for example, CdS/ZnS, CdSe/CdS, etc[2, 87, 117]. The shell functions as a barrier for charge carrier tunnelling into the matrix and reduces the concentration of dangling bonds at the QD interfaces.
Currently, the size effect in exciton luminescence has been demonstrated for quite a number of compounds such as ZnS QDs in the 300 – 380 nm wavelength range, CdS QDs (380 – 460 nm), ZnSe QDs (360 – 500 nm), CdSe QDs (480 – 660 nm), CdTe QDs (600 – 1000 nm), InP QDs (650 – 750 nm), PbS QDs (700 – 1600 nm), PbSe QDs (1000 – 2500 nm), Si QDs (400 – 750 nm) and Ag2S QDs (400 – 900 nm)[51, 101, 102, 136, 386, 387, 394, 395, 425-430].
As regards colloidal QDs, CdS nanocrystals with sizes of 2 – 5 nm synthesized in hydrophilic colloidal solutions among the first systems that exhibited strong exciton luminescence[41-43]. Broad options for varying the QD size and size distribution in an ensemble were demonstrated for the synthesis in TOPO (CdSe, CdS and CdTe QDs)[51]. It was necessary, however, to explain the magnitude of the Stokes shift for exciton luminescence in CdSe QDs (up to ~20 nm) and its dependence on the size[99, 368] and the proniunced increase in the lifetime of luminescence up to the microsecond range upon thermalization. First, the observed features were attributed to the involvement of surface states in the emission[99, 431]. Later, the Stokes shift for exciton luminescence was substantiated[56, 93] by splitting of the ground state of the exciton into bright and dark states due to the electron– hole exchange interaction, which is more intense in QDs than in bulk crystals due to the quantum confinement. A system of energy states and optical transitions in the absorption and luminescence of CdSe QDs compiled using published data[56, 93] is presented in Figure 10.
According to published data[56, 93], splitting into light and dark states of the exciton provides a Stokes shift of the luminescence band relative to the ground exciton absorption. For binary semiconductors, the valence band is often described by p-like atomic orbitals. This ensures the formation of three subbands for holes (heavy, light, and split-off holes). In this case, the total angular momentum for the exciton with the lowest energy is the sum of the total angular momenta of its constituent electron (\( J_e = l + s = 0 + 1/2 \)) and heavy hole (\( J_{hh} = l + s = 1 + 1/2 \)). The total angular momentum for the exciton \( J = J_e + J_{hh} \), equal to unity, corresponds to the optically active (light) state, while \( J = 2 \) corresponds to the optically inactive (dark) state of the exciton. Optical transitions (absorption and luminescence) involving the dark state are forbidden in the dipole approximation (\( \Delta J = 2 \) and \( \Delta S = 1 \)), while those involving the light state (\( \Delta J = \Delta L = 1 \), \( \Delta S = 0 \)) are allowed (see Figure 10. Thus, the absorption will be dominated by the transition to the state with \( J = 1 \). In the luminescence, due to the fast thermalization of the exciton to the \( J = 2 \) state, the transition from this state to the ground state will predominate, although this transition is forbidden, which ensures the lifetime of luminescence in the microsecond range for CdSe QDs at 5 K[432].
In the calculations made in the effective mass approximation and perturbation theory, the electron – hole exchange interaction for QDs under quantum confinement was expressed as[93]
where \( \hat{\sigma} \) is the electron Pauli matrix, \( \hat{J} \) is the hole Pauli matrix, \( a_0 \) is the lattice constant, and εexch is the exchange strength constant (~320 meV for CdSe). The calculated splitting between the light and dark states in CdSe QDs was 12.5 meV, which is two orders of magnitude larger than the corresponding value for a bulk crystal (0.13 meV). This approach made it possible to qualitatively explain the Stokes shift between the exciton in absorption and the exciton in luminescence within a range of 1 – 20 meV (see Figure 10).
By taking into account the projection of the total angular momentum onto a selected direction (the C axis in a wurtzite type crystal lattice and QD non-sphericity)[56, 93] enabled quantitative determination of the Stokes shift. Moreover, in this case, it was possible to explain the sharp increase in the lifetime of luminescence with decreasing temperature. For CdSe QDs, it was shown that allowance made for the shape anisotropy and the intrinsic crystal field leads to further splitting of the light and dark exciton into five sublevels and emergence of a hyperfine structure[93]. The projection of the total angular momentum M gives states ± 2, ± 1, and 0 for \( J = 2 \) and ± 1 and 0 for \( J = 1 \). Thus, the initially eightfold degenerate exciton (1S3/21Se) is split into five states (see Figure 10). The designations correspond to those used by Nirmal et al[93].
The selected directions are both the symmetry axis \( C \) in the hexagonal crystal lattice and the axis of the ellipse, which reflects the shape of the QD and its non-sphericity. These factors are additive and lead to the common splitting into a hyperfine structure[93]
where \( \Delta_{\text{int}} \) is the crystal field splitting; \( \Delta_{\text{asym }} \) is the splitting arising from QD ellipticity; \( \beta_m \) is the ratio of the effective masses of heavy and light holes along the \( C \) axis in a bulk semiconductor; \( R \) is the QD radius, and \( \gamma = c/b \) is the degree of ellipticity (\( c \) and \( b \) are the major and minor semiaxes of the ellipse).
For this arrangement of sublevels, the projection of angular momentum of the lowest exciton state along the crystalline \( C \) axis is \( M = 2 \), and this state is optically inactive. Hence, at the helium temperature, emission occurs either through a longitudinal optical (LO) phonon transition or through a spin-flip transition involving interactions with paramagnetic centres (for example, surface dangling bonds)[433]. At high temperatures (T > 100 K), due to thermal population of the next state with \( M = 1^L \), the emission occurs from this state. The splitting between the levels ± 2 and ± 1L is 2 – 3 meV, and it is not detected in most studies.
Investigation of the luminescence excitation spectra for single CdSe QDs revealed several narrow most intense lines, which could be correlated with particular exciton sublevels[94]. Transitions involving these levels are depicted in Figure 10. It turned out that the formation of the Stokes shift involves the ± 1L and 0L levels with a longitudinal optical phonon (the total angular momentum for them is equal to 2; these levels are all dark) and ± 1U and 0U levels (the total angular momentum is 1; these levels are all light). It is noteworthy that in the literature, the 1L state is often called light exciton, which leads to considerable confusion and lack of explanation for the Stokes shift.
Thus, the size dependence for the exciton luminescence spectra of QDs with a hexagonal crystal structure (e.g., CdSe QDs) and a large spin – orbit splitting is determined by the size dependence of the absorption spectra and the energy of the exchange interaction between the electron and hole in the exciton, taking into account the non-sphericity of the QD and the crystal field[93, 432-435].
Exciton luminescence of CdSe QDs with a small Stokes shift (≈ 20 meV) of the luminescence band maximum relative to the maximum of the long-wavelength absorption band can also be observed in the case of synthesis in reverse micelles[103]. Recording the band edge luminescence spectra upon excitation with emission corresponding to the long-wavelength edge of the absorption spectrum made it possible to minimize the inhomogeneous broadening of the luminescence spectrum, which in this case consisted of a set of narrow peaks, phonon repetitions, involving the LO phonon in CdSe (~ 210 cm–1). However, in this case, too, the shortest-wavelength luminescence line was shifted from the luminescence excitation band. For some period of time time, there was the opinion that the Stokes shift for edge luminescence was associated with the localization of a hole at the QD surface level belonging to a three-coordinate Se atom[99, 368]. Calculations using the tight binding method showed that this localized state was situated slightly above the valence band top[436]. Despite the success achieved in the synthesis of CdSe QDs in reverse micelles, band edge luminescence in them was observed only at temperatures below room temperature. Thus, it was found that the size dependence of the exciton luminescence of CdSe QDs is determined by the size dependence of the exciton transition in the optical absorption, while the magnitude of the Stokes shift is primarily determined by the fine structure of the exciton and slightly depends on the size.
For CdS QDs with a cubic lattice, the spin – orbit splitting is small. The magnitude of the exchange interaction for CdS QDs is approximately 10 meV[71]. The Stokes shift of 20 – 70 meV observed in the experiment cannot be explained using the model that describes the exciton fine structure in CdSe. In terms of the \( k \cdot p \) theory, it was found that the lowest-energy absorption is forbidden for small CdS QDs, since the ground state of the envelope wave function of the electron is s-symmetric, while that of the hole is p-symmetric[48, 372, 381]. The next transition in the absorption involves s-like envelopes of hole wave functions and is allowed. This approach was used to interpret the size dependence of the Stokes shift and the lifetime of luminescence at low temperatures[373]. For large CdS QDs, the sequence of s- and p-like hole levels changes, and the lowest energy transition becomes allowed.
For colloidal CdTe QDs, even those obtained by low-temperature hydrophilic synthesis, exciton luminescence with a high quantum yield is observed in the absence of a recombination component, which indicates a relatively low concentration of defects[200]. For CdS QDs with a hexagonal crystal lattice, an explanation of the Stokes shift of the exciton luminescence is similar to the case of CdSe QDs[370, 437]. This approach is used to explain the temperature behaviour of the intensity of exciton luminescence, the lifetime of which increases with increasing temperature[435, 438].
Analysis of exciton luminescence in QDs of other compounds is faced with difficulties even in substantiation of the nature of this luminescence. For example, for Ag2S QDs the problem of the Stokes shift has not been addressed in detail due to the lack of data on the fine structure of the exciton ground state. This is apparently due to the complex crystal structure, which has low symmetry (monoclinic lattice). Meanwhile, there are data[132, 413] on the formation of monodisperse Ag2S QDs of average size ranging from 1.5 to 4 nm for which a similar relationship was found between the positions of the luminescence peaks and exciton absorption with a Stokes shift (50 – 70 nm). The luminescence of these samples occurs at the long-wavelength boundary of the visible and near-IR ranges (500 – 900 nm). The luminescence bands have a half-width of about 0.1 eV and can be attributed to the radiative annihilation of excitons.
For luminescent colloidal QDs doped with various atoms and ions, the dopant atom (or ion) or its local coordination sphere acts as the luminescence centre. Luminescence occurs as a result of optical transitions between the states of the impurity centre[412]. The observed luminescence band turns depends only slightly on the QD size. The size effect acts, first of all, on the structure of excitation spectra, luminescence kinetics and the efficiency of excitation of intracentre luminescence.
In some cases, the selection rules for forbidden intracentre transitions may change due to the orbital mixing (for example, d – p mixing) and the formation of hyperfine structure under the action of crystal or ligand field. The problem of doping of QDs with Mn2+ ions has been considered most comprehensively for ZnS QDs. The appearance of a new narrow luminescence band in the 580 – 590 nm range, characteristic of a spin-forbidden transition from the 4T1 (4G) excited state to the 6A1 (6S) ground state of Mn2+, was reported[439, 440]. If Mn2+ ions are incorporated into the lattice of ZnS nanocrystals, this transition is characterized by a high luminescence quantum yield and luminescence lifetime of 3.3 ms[440]. In recent years, many researchers have successfully obtained Mn2+-doped ZnS QDs by the synthesized in reverse micelles[440], aqueous synthesis in thiocarboxylic acids[441], in polyvinylpyrrolidone[442], etc.
The quality of doping affects the luminescent properties of QDs. It was shown[443] that the emission from manganese ions is due not only to the Mn2+ ions incorporated in the ZnS nanocrystal. The long-wavelength tail of this emission may arise from Mn2+ ions in the oxidized and hydrolyzed regions of the nanocrystal interface. The substituting manganese ions were found to be localized in zinc positions subject to the local axial distortion of the lattice[444]. The energy of the internal 4T1 – 6A1 manganese transition depends on the distance between the Mn2+ ions and the ligands[445]. Pradhan[446] has shown that the spectral emission characteristics of Mn2+ can be controlled by changing the chemical composition of the QDs or by fabrication of complex core/shell/shell structures. The time-resolved transient absorption method was used to determine the time of energy transfer from the QD exciton to manganese (~ 60 ps) in spherical CdS/ZnS QDs doped with manganese[447].
Currently, ways to enhance the photoluminescence efficiency of Mn2+-doped ZnS : Mn2+ QDs are actively discussed. Jiang et al.[448] used a Zn(OH)2 shell formed at the interfaces of ZnS : Mn2+ QDs. The luminescence intensity of ZnS : Mn2+ QDs can be increased by long-term UV irradiation[449]. In addition, it was found that doping ZnS : Mn2+ with Eu2+ ions increases the intensity of the manganese emission band by a large factor[450]. A similar result was obtained when Au particles were added to ZnS : Mn2+ QDs[451].
It was also shown that QDs of mixed composition ZnxCd1–xS : Mn2+ are more convenient for application, since there is no need to use ultraviolet sources to excite Mn2+ radiation[452]. Most studies in this area are focused on only the development of synthesis and optimization of luminescence of ZnxCd1–xS : Mn2+ QDs. However, neither models of photophysical processes that provide luminescence of ZnxCd1–xS nor the interaction of recombination luminescence centres and luminescence at the Mn2+-based centres in these QDs were discussed.
The effect of Mn2+ doping of colloidal CdS QDs on the kinetics of luminescence cused by the forbidden d – d transition with a luminescence lifetime of the order of a millisecond was demonstrated[453]. For ZnxCd1–xS QDs, non-radiative transfer of electronic excitation energy from recombination luminescence centres to Mn2+ ions with an efficiency of 0.24 – 0.30 was discovered[454].
The development of QD synthesis brought about the questions of whether doping of QDs with rare earth element (REE) ions is feasible and how this would affect the size-dependent luminescent properties. Doping may provide not only the additivity of the size-dependent luminescent properties of QDs and well-luminescent rare earth ions, but also new hybrid properties that are not characteristic of single components[455]. An increase in the luminescence quantum yield of rare earth elements is also probable. Today, substantiation of the mechanisms of luminescence of rare earth ions upon excitation of QDs and the model of interaction between radiative recombination centres and rare earth ions is still relevant[456, 457].
Among the rare earth elements, Eu3+ ions occupy a special place as dopants of this type. They are characterized by narrow luminescence peaks in the red region (near 615 nm)[456-458] and a magnetic response[459]. Currently, determination of the conditions for incorporation of Eu3+ ions into QDs to provide intense luminescence is a challenging problem[460-462]. In particular, it is necessary to study the interaction between recombination luminescence centres of QDs and Eu3+ doping ions[455]. It is assumed, for example, that electronic excitation is transferred from the recombination luminescence centres of ZnO nanocrystals to Eu3+ ions[457]. It is also necessary to take into account the probability of transfer of charge carriers from the photoexcited matrix to the rare earth ion. For Eu3+-doped CdS nanocrystals with an average size of 8 – 10 nm and a hexagonal crystal structure, luminescence was detected for the 5D0 – 7F1 and 5D0 – 7F2 transitions[463]. It was found that an increase in the Eu3+ concentration induces a shift in the intrinsic luminescence band of CdS, a sharp increase in the magnetic response[463], and a decrease in the interplanar distances[464].
An attempt was made to dope colloidal QD CdS with Eu3+ ions obtained from europium β-diketonate complex, which, in turn, was synthesized from europium chloride and [4,4,4-trifluoro-1-(thiophen-2-yl)butane-1,3-dione] (TTA)[465]. The most preferred design, CdS/Eu3+ TTA/TGA QD, in which Eu3+:TTA is localized on the QD surface also occupied by thioglycolic acid (TGA) molecules, was spectrally justified. A significant increase in the lifetime of luminescence, from 190 to 346 μs, in the Eu3+ luminescence band (615 nm) was observed upon the complex assembly. In such systems, non-radiative energy transfer from the recombination luminescence centres of CdS QDs to Eu3+ ions was detected.
Thus, doping with rare earth and transition metal ions, in particular Eu3+ and Mn2+, has not yet provided full control over the luminescence of semiconductor QDs. There are no general approaches to targeted doping of QDs to ensure the population of nanocrystals with impurity ions and effective passivation of QD interfaces, while preserving the structure of complexes that sensitize rare earth ions. The problem of interaction between luminescence centres generated by intrinsic QD defects and the doping ions remains unsolved.
Apparently, the largest group of luminescent colloidal QDs are those the luminescence of which is characterized by a noticeable Stokes shift exceeding 0.2 eV and a significant half-width of the emission band (see [51, 87, 108, 109, 131, 132, 139, 146, 147, 184, 198, 232, 334, 345, 347, 399, 435, 100-102, 341-343, 413-422, 466-471]).
Recombination luminescence occurs as a result of optical transitions between QD energy states and localized states due to both impurity atoms and ions and intrinsic defects located inside the nanocrystals and at their interfaces, including matrix states[65, 123, 124, 182, 183, 472-474]. Depending on the type of defect or impurity, the state can be a donor (with an excess of electrons) or an acceptor (with a deficiency of electrons). These localized states are conventionally divided into shallow and deep levels. Shallow levels are located near the QD electronic states, and even if they do not directly participate in luminescence, their properties can be studied using thermally stimulated luminescence method[106, 475]. Deep levels provide a strongly bound state for non-equilibrium charge carriers. They are characterized by both radiative and non-radiative recombination. The arising luminescence can be used to determine the energy of trap states within the effective band gap. The energies of localized states not involved in luminescence are directly determined through the effects of photo- and thermally stimulated luminescence[102, 106, 475, 476].
It has now been established that the formation of trap states within the effective band gap associated with the levels of structural impurity defects, which operate as centres of both luminescence and non-radiative recombination, has a significant impact on photoprocesses used in various areas[79, 102, 84-86, 477-481]. In some cases, the presence of luminescence centres and traps of various depths is useful. For example, localized states and levels of QD recombination luminescence centres determine low-threshold optical non-linearities (non-linear absorption and refraction) of pico- and nanosecond pulses, which is useful for the design of power limiters and systems for protecting eyes and devices from laser damage, radiation phase control systems in adaptive optics, etc[482, 483]. This is exemplified by colloidal Ag2S and PbS QDs[484, 190-195]. In other cases, for example, in photovoltaics for the design of solar cells and in QD-based photodetectors, the localized states of radiative and non-radiative recombination centres have an adverse effect. They are usually removed by improving the conditions for crystallization and passivation of QDs. However, even in the latter case, the intensity of recombination luminescence, proportional to the concentration of luminescence centres, is important, since it serves as an indicator of these adverse trap states.
Recombination luminescence bands were observed in some early successful experiments on the synthesis of colloidal CdSe and CdS QDs. Along with narrow peaks, for which the Stokes shift was 2 – 25 meV, broad structureless luminescence bands were observed[55, 56, 100]. The latter were attributed to radiative transitions at the levels of structural impurity defects. As the average size of CdS nanocrystals synthesized in glass decreases, a complex transformation of the photoluminescence spectrum occurs; the spectrum of 140-nm particles exhibits an exciton peak and a set of luminescence bands associated with recombination[100]. If the particle size decreases down to 7 nm and less, the intensity of the recombination luminescence bands increases. The luminescence spectrum of CdS QDs with a size of approximately 3 nm is dominated by luminescence driven by transitions between defect levels[100]. For CdSe QDs, the recombination component in the luminescence spectrum always occurs as a parasitic effect, which can be successfully suppressed.
Thiols were used to passivate CdS QDs[485] in the synthesis of highly dispersed assemblies with recombination luminescence. An interesting result was obtained by Kim et al.:115 the surface treatment of CdS QDs synthesized by the reverse micelle method with a Cd(ClO4)2 solution and a NaOH solution to adjust the pH level resulted in the formation of a Cd(OH)2 shell on the QD surface and an increase in the narrow short-wavelength luminescence bands, which corresponded, in the authors’ opinion, to annihilation of excitons. A decrease in the concentration of dangling bonds in CdS QDs as a result of effective passivation led to decreasing intensity of the recombination component[218, 486]. The complex structure of the luminescence spectrum of CdS QDs with an average size of 4.4 nm passivated with oleic acid was demonstrated[102]. When colloidal solutions were cooled down to 10 K, three new recombination bands with maxima at 2.15, 1.76 and 1.37 eV appeared in the photoluminescence spectrum of these QDs, in addition to the exciton luminescence with a maximum at 2.66 eV. An original diagram of radiative transitions giving rise to these bands was substantiated. For QDs synthesized in gelatine, it was possible to detect the size effect in the recombination luminescence spectrum and to show that a significant contribution to the inhomogeneous broadening of the recombination band is made by not only the size dispersion of QDs, but also dispersion of donors and acceptors in single nanocrystals involved in recombination[105].
Thus, in the case of CdS QDs, the predominant contribution of the recombination component is due to a rather high concentration of traps with different charge and energy properties, associated with significant non-stoichiometry[487-491]. Only in exceptional cases, it is possible to achieve exciton luminescence in CdS QDs. Colloidal CdS QDs synthesized in an aqueous medium are characterized by luminescence at defect levels, even when they are encapsulated in a ZnS shell[487]. It should be noted that, in some cases, with careful optimization of synthetic procedures in low-toxic media, a high quantum yield (up to 70%) of recombination luminescence is achieved[108].
Other vivid examples of compounds with pronounced recombination luminescence are Ag2S and Ag2Se QDs[104, 107, 350, 355, 356, 393, 415-421, 492-503]. For colloidal Ag2S QDs, unambiguous understanding of the size effect in luminescence spectra and the nature of the Stokes shift is an obvious challenge. Only a few works (e.g.,[132, 466]) have reported the formation of monodisperse Ag2S QDs with exciton luminescence. In other cases, recombination luminescence in the 660 – 1200 nm range is predominantly observed. The strong influence of the conditions of synthesis and passivation of Ag2S QDs on the luminescence nature and size dependence was found. It was suggested that the slow supply of sulfur into the growth zone of nanocrystals at temperatures above 323 K (50 °C, pH = 7 – 10) ensures the synthesis of small highly dispersed particles[132, 492]. The sulfur precursor, sodium sulfide Na2S, facilitates the formation of nanoparticles with a high sulfur content on the surface, accompanied by their growth and the emergence of localized states[393]. This conclusion was confirmed by Ovchinnikov and co-workers[192, 493]. It was shown that an increase in the concentration of sulfur atoms upon introduction of a sodium sulfide solution into a solution of Ag2S/TGA QDs during the synthesis facilitates the formation of IR recombination luminescence centres (660 – 1000 nm) and suppression of exciton luminescence (620 nm). Thus, the absorption and luminescent properties of Ag2S QDs are determined by the precursors used, which stabilize the colloidal solution with organic shells or polymer molecules.
For Ag2S QDs, an unambiguous understanding of the size effect in recombination luminescence spectra has only started to appear. Often, due to the absence of a maximum or a clearly pronounced feature of the main exciton absorption transition, it is difficult to assign the observed luminescence band to a particular type on the basis of the Stokes shift[131, 146, 390, 392, 415, 416].
Some data on recombination luminescence of Ag2S QDs in gelatine are available[83, 106, 192, 197]. Their IR luminescence maxima are located in the range of 1000 – 1200 nm and have a weak size dependence. The properties of recombination luminescence for Ag2S QDs passivated with mercapto acids have been studied in most detail. The size dependence of the luminescence of Ag2S QDs passivated with thioglycolic acid was identified[83, 493]. The size effect in the IR luminescence of Ag2S QDs turned out to be much weaker than that in optical absorption. Smirnov and Ovchinnikov[107] integrated data on the size effect in the spectra and luminescence kinetics for five types of samples of colloidal Ag2S QDs dispersed in polyvinyl-pyrrolidone, gelatine, and passivated with thiocarboxylic acids, including thioglycolic acid, 2-mercaptopropionic acid and L-cysteine. These data provided conclusions about the general mechanism of luminescence in Ag2S QDs.
The size dependences of the luminescence spectra of colloidal Ag2Se QDs synthesized by various methods using various precursors do not exhibit any correlations[494-497]. However, the contribution to the observed luminescent properties of Ag2Se QDs from structural defects due to the non-stoichiometry of Ag2Se and the quality of passivation of QD interfaces has not yet been identified. It should be noted that Ag2Se is a compound with a significant degree of non-stoichiometry. In most cases, it exists as the Ag2+dSe phase where d ranges from –0.05 to +0.03[498-500]. This circumstance suggests that the luminescence of localized states would prevail over the exciton one. However, it is still very difficult to identify the contributions of different mechanisms of Ag2Se QD luminescence to the general picture of the size effect. The situation is significantly complicated by the formation of complex compounds, for example, Ag2SexS1–x, since thiol-containing components are used[501]. For the luminescence of Ag2Se QDs, it is nevertheless possible to distinguish exciton emission with a small Stokes shift and emission with a relatively large (about 1 eV) Stokes shift. A study of the luminescence of colloidal Ag2Se QDs passivated by 2-mercaptopropionic acid confirmed this assumption[502]. An increase in the concentration of the selenium precursor and a decrease in the sample temperature to 80 K were found to enhance luminescence in the long-wavelength recombination band (840 – 890 nm) with simultaneous pronounced quenching in the short-wavelength exciton band (715 – 720 nm). Despite numerous studies addressing the size effect in luminescence for colloidal PbS QDs, the overall picture remains complex and contradictory. Due to the quantum size effect, decrease in the crystal size from 20 to 1 nm makes it possible to tune the absorption and luminescence bands to the IR and visible ranges[503-510]. However, currently there is no common opinion regarding the mechanism of the resulting luminescence (Figure 11)[511]. It has been shown that with decreasing PbS QD size, the Stokes shift for luminescence increases linearly, in direct proportion to the exciton absorption energy in accordance with the empirical formula
For \( E_{g}^eff = 1.13 \text{eV} \), the Stokes shift is zero. However, in this work, the QD size was not determined. For PbS QDs with an exciton energy of 1.13 eV, the average size was reported to be about 4 nm[366, 367]. Thus, these arguments lead to the paradoxical conclusion that for PbS QDs with an exciton energy less than 1.13 eV (i.e., with an average size of more than 4 nm), the Stokes shift is negative. Later, Fernée et al.[504] explained the observed empirical dependences using a model of radiative recombination of a localized charge carrier with a free carrier of the opposite sign. In this model, for PbS QDs with an exciton absorption transition energy of less than 1.13 eV, this localized state was found to be located above the quantum size states of the nanocrystal (pseudo-trap state); the luminescence becomes exciton luminescence, and the Stokes shift decreases to almost zero. Additionally, a negative Stokes shift was found for a series of PbS QDs in glass with exciton absorption peaks at 1851, 2004 and 2043 nm, which corresponds to QDs with average sizes of 8.3, 9.2 and 9.5 nm, respectively[503]. For the smallest PbS QDs of 3.6 – 3.7 nm size, the Stokes shift is as large as 0.45 – 0.50 eV[503]. For PbS QDs with an average size of about 2 nm and an exciton absorption peak at 560 nm (2.21 eV), a Stokes shift of 0.39 eV was observed[505], which is markedly smaller than the values reported in other studies[503, 504].
Previously, analysis of the temperature dependence of the position of luminescence peak and exciton absorption and data from time-resolved luminescence spectra led to the conclusion that the luminescence band contains three components[506]. All of them were attributed to radiative recombination of charge carriers located in shallow traps of charge carriers. The detected Stokes shifts were 0.47, 0.25 and 0.08 eV, respectively. In some studies, for example, in a study by Nakashima et al.[508], no data on the absorption spectra and the magnitude of the Stokes shift were given for PbS QDs with an average size of about 7 nm and a luminescence peak at 1300 nm; therefore, the observed luminescence was not classified as exciton or recombination luminescence. For PbS nanocrystals in glass, it was found that for the peak of the exciton absorption transition with energy ranging from 0.8 to 1.4 eV, the Stokes shift slightly depends on the size and does not exceed 0.12 eV[509]; this is markedly smaller than the values reported in other studies[504, 505, 510]. In the case of PbS QDs passivated by thioglycolic acid, the Stokes shift between the exciton absorption and luminescence peaks increases from 0.086 to 0.32 eV with a decrease in their average size from 4.9 to 2.6 nm. This trend was interpreted as an increase in the energy of the Coulomb interaction between an electron and a hole in an exciton due to quantum confinement of charge carriers[511]. The kinetics of luminescence decay, which is non-exponential, includes a fast and a slow component. The time constant of the slow component, which slightly depends on the average QD size, is in the 4.4 – 5.6 μs range. Considering the distribution of the defects acting as luminescence quenchers in QDs over the ensemble made it possible to relate the slow component to the radiative recombination constant in PbS QDs without quenchers. As a result, it was concluded that the observed size-dependent luminescence of PbS QDs passivated with thioglycolic acid is determined by exciton radiative recombination[511].
Thus, increase in the contribution of recombination luminescence is typical when the colloidal synthesis of QDs is carried out in an aqueous medium using various passivating agents and stabilization of nanocrystals in an inert polymer (gelatine, polyethylenimine, polyvinyl alcohol, etc.), which ensure the hydrophilicity and low toxicity of colloidal solutions required primarily for biological applications[100, 102, 108, 232, 435, 512]. However, the presence of a recombination luminescence band is usually indicative of a low quality of passivation of the QD surface[117]. Considerable efforts by various research groups are aimed at suppressing this luminescence, for example, by optimizing the passivation conditions[80, 435, 513, 514] and forming core/shell structures in which colloidal QDs are coated with a semiconductor with a larger band gap, for example CdS/ZnS, Ag2S/ZnS, CdSe/CdS, etc[114, 117]. According to some studies, a high luminescence quantum yield can be attained for the recombination band under certain conditions of CdS QD crystallization[108]. There is also indirect evidence in favour of the formation inside nanocrystals of defect interfaces, which are relatively insensitive to passivation conditions, in concentrations that are noticeably higher than that obtained by high-temperature synthesis[476].
The above brief discussion of the main absorption and luminescence patterns of the size effect in QDs indicates that it is much more complex for recombination luminescence than for exciton luminescence. To explain this result, it is important to understand the nature of the Stokes shift and substantiate the mechanism of radiative recombination. It is apparent that the nature of Stokes shift for recombination luminescence bands is different from that for exciton luminescence. The size dependence of the Stokes shift may involve the influence of confinement on the energy states of the valence band, conduction states and defect levels. Analysis of the structure of the corresponding photoluminescence band revealed a contribution of inhomogeneous broadening and underlying physical processes. Many of the questions raised here can be addressed by determining the specific mechanism of recombination luminescence. Like in the case of luminescent mono- and polycrystalline semiconductors, this problem for colloidal QDs is highly challenging.
For the first time, the mechanism of the size dependence of recombination luminescence was consistently analyzed for CdS QDs immobilized in glasses[100]. A comparison of the size dependence of the luminescence band maxima and the results of evaluation of the size effect for electrons and holes in the effective mass method for CdS QDs provided the conclusion about the donor–acceptor (DA) nature of recombination in bands with a Stokes shift of approximately 0.4 and 1.0 eV. It should be noted that this result had a complex interpretation due to the non-elementary nature of the luminescence band, which was associated with the variety of structural defects participating in the transitions. Some of them are attributed to transitions involving only donor or only acceptor levels of luminescence centres. An apparent challenge to this study is the noticeable size dispersion of CdS QDs grown in glasses. Katsaba et al.[102] analyzed the luminescence mechanism of colloidal CdS QDs passivated with oleic acid, which also showed a complex spectral structure, and the temperature dependence of the luminescence intensity of the components studied in the range from 4.2 to 300 K and proposed a model of optical transitions, which included DA-recombination and recombination of a free electron with a localized hole. a A mechanism for luminescence on DA pairs was also proposed for CdS QDs[101, 413], considering luminescence quenching by charge acceptor molecules; however, the size dependence of luminescence was not addressed in these works.
Ovchinnikov et al.[105] found experimental facts indicative of the DA mechanism of recombination luminescence in colloidal CdS QDs of medium size ranging from 1.7 to 5.8 nm dispersed in gelatine and passivated with thioglycolic acid. The first fact was a weak dependence of the position of the exciton absorption peak in the excitation spectra of CdS QD ensembles on the wavelength of luminescence measurement. This situation is likely if non-equilibrium charge carriers are involved in the recombination of donors and acceptors. The distribution of DA pairs in QDs over the distance between the donor and the acceptor and the size distribution of QDs account for a slight change in the position of the luminescence excitation peak (0.2 eV), whereas the energy of the detected luminescence quantum changes noticeably (1.0 eV). The second experimental fact is the red shift of the maximum of the luminescence band when the of CdS QD luminescence decays over a nanosecond time interval. The highest energy of luminescence quantum was found for transitions with the shortest distances between donors and acceptors in CdS. The energy of the luminescence quantum on DA pairs was determined using the following expression[105]:
where \( E_d \) and \( E_a \) are the binding energies of the donor and the acceptor, \( \varepsilon \) is the dielectric constant, and \( r_d - r_a \) is the distance between the donor and the acceptor.
Therefore, as luminescence decays, only the DA pairs in which the donor and the acceptor are most remote from each other have not yet emitted light; this accounts for a long-wavelength shift of the luminescence band during the decay. In addition, a retardation of the luminescence decay at the emission band maximum with increasing average QD size was noted; this also confirms the mechanism of DA radiative recombination, since the larger the QD size, the longer the average distance between the donor and the acceptor[329]. Finally, the size dependence of the energy of luminescence maximum does not contradict the model of recombination on DA pairs. This dependence resembles most closely the size dependence of the electron energy in the conduction state. However, the slopes of these dependences in the \( E(R)^2 \) coordinates are slightly different, which is due to the contribution of the size effect for localized electrons and holes to the size dependence of luminescence, similarly to the data of Ekimov et al[100]. The inhomogeneous broadening for luminescence caused by recombination on DA pairs was also analyzed by Ovchinnikov et al[105]. The authors concluded that it is necessary to take into account the distribution of donors and acceptors over the depth of states within the effective band gap and the influence of confinement on both a shallow donor (weakly bound electron) and a deep acceptor (strongly bound hole).
Further analysis of the size dependence of the energies of radiative recombination transitions, along with the size effect of the eigenstates of a nanocrystal, makes it possible to substantiate other radiative recombination mechanisms, for example, those in which either the donor or the acceptor is involved in the transitions. This concept is depicted in Figure 12.
This approach was successfully used to substantiate the mechanism of recombination luminescence in colloidal Ag2S QDs passivated with various thiocarboxylic acids and dispersed in polymers[107]. It was found that the weak size effect in the IR luminescence of all studied Ag2S QD samples is attributable to the weak size dependence of the positions of energy states in the valence band and to the fact that luminescence is due to radiative recombination of a hole with an electron trapped at the luminescence centre. However, it should be noted that the approach used by Efros and co-workers[100] and Ovchinnikov and co-workers[105, 107] is inapplicable to QDs with the same extrema of the Brillouin zone for holes and electrons, i.e., with the same size effect (for example, PbS, PbSe, etc.).
3.3. Specific features of exciton dynamics
The absorption and luminescence studies provide information about the static picture of luminescence. However, the dynamics of excitons determines the stages of photoprocesses that occur after QD excitation, including luminescence, non-radiative transfer of electronic excitation energy, various charge capture and transfer processes, etc. The processes considered below are related to the incoherent dynamics of electronic excitations[435, 515-544].
Since colloidal QDs of most of the studied compositions feature a high oscillator strength of optical transitions, the relaxation processes of electronic excitations are investigated in the femto-, pico-, nano- and microsecond ranges.
Apparently, most information is provided by the time-resolved transient absorption spectroscopy (pump – probe method), which has been successfully used to explore the dynamics of excitons in various QDs[515-540]. According to this method, pump pulses excite charge carriers, thus changing the optical absorption of QDs, while time-delayed probe pulses are used to detect the changes in absorption. Analysis of the evolution of the spectral distribution of the transient absorption makes it possible to follow the sequence of processes that occur in time period from the QD photoexcitation and exciton formation up to the final exciton decay via direct annihilation or recombination at the levels of structural impurity defects (radiative or non-radiative). This method assumes that the sample is optically homogeneous and weakly scattering.
Another popular method for time-resolved spectroscopy is photoluminescence kinetics, which covers both the enhancement (population of the luminescent state) and decay (relaxation of carriers from excited states) of luminescence intensity.
After the formation of theoretical and experimental concepts about the discrete electronic structure of quantum dots, for which the distance between the electron size quantization levels noticeably exceeds not only \( kT \), but also the phonon energy in the corresponding substance, a low rate of photon emission, i.e., thermalization of highly excited electrons and holes, was theoretically predicted[545, 546]. This limitation was called the phonon bottleneck effect. It was theoretically shown that the thermalization of electrons should be markedly slower in a QD than in a bulk crystal, quantum wire or quantum well. As opposed to the results obtained by Bockelmann and Bastard[545] or Benistry et al.[546], it was theoretically predicted[547] that electrons in QDs can effectively relax due to Auger energy transfer to electron plasma even in small semiconductor quantum dots, where relaxation due to phonon scattering is weak. However, the details of such Auger processes for colloidal QDs under single-quantum excitation were not entirely clear.
Despite the predicted slow thermalization of charge carriers for CdSe QDs, the application of the pump – probe technique made it possible to experimentally establish that the electron thermalization rate from the excited 1P state to the ground 1S conduction state occurs entirely within 300 fs[525]. It was difficult to obtain experimental data on the dynamics of a photoexcited hole due to the high density of hole states.
Somewhat later, Efros et al.[548] theoretically proposed an Auger-like mechanism of rapid energy transfer from electrons to holes in the valence band; the probability of this mechanism is higher in nanometre-sized QDs than in bulk crystals due to the Coulomb interaction of carriers enhanced by the quantum confinement. The authors theoretically showed that the time of electron thermalization from the first excited 1P state to the ground 1S state is ~ 2 ps.
The most direct experimental evidence for the Auger process and its role in electron thermalization was obtained for CdSe QDs by Guyot – Sionnest et al[549]. They reported the first study of the intraband relaxation rates of 1P to 1S electronic states in CdSe QDs in the strong confinement mode. The authors used an upgrared pump – pump – probe technique. After excitation to the exciton ground state (1S3/2 – 1Se transition), the sample was illuminated with an IR pulse with an energy close to that of the 1Se – 1Pe transition, and the 1Se – 1Pe relaxation dynamics was scanned with the probe beam. The replacement of the tri-n-octylphosphine oxide ligand molecule by thiocresol or pyridine made it possible to detect a significant decrease in the rate of electron thermalization for QDs with organic ligands that effectively capture a hole and, thus, block the electron – hole Auger process. The characteristic time of electron thermalization in such QDs was found to be ~ 200 ps(!), and the electron relaxation rate was < 1 meV ps–1, which is two orders of magnitude slower than that for bulk crystals. Thus, it was convincingly demonstrated that when an exciton in CdSe QD is excited to a high-energy state, the hole undergoes rapid relaxation in 200 – 500 fs[94, 542, 543, 520-522]. Despite significant energy distances between size quantization levels exceeding tens of LO phonon energies, the electron relaxation also occurs in sub-picosecond time intervals[94, 518, 543] due to the strong electron – hole interaction in the confined exciton. This interaction increases with decreasing nanocrystal size, as does the overlap integral of the electron and hole wave functions[94, 434, 517, 521, 542-544].
One of the competing relaxation processes of hot excitons is the direct capture of a hot exciton by surface traps[517, 519, 523, 524].
After rapid intraband relaxation of the exciton to the ground state, electronic excitation further decays through several competing channels. The first of them is radiative exciton annihilation, which is the slowest process. The radiative luminescence lifetime for CdSe QDs at room temperature is 10 – 15 ns[527, 550]. The duration sharply depends on temperature[527] and varies in a nano- and microsecond time range[527]. The second channel is recombination, both radiative and non-radiative, involving traps[551]. The ratio of the probabilities of all the above processes (radiative exciton annihilation, radiative and non-radiative recombination) is determined by the quality of nanocrystals, the presence of passivating shells made of organic surfactants, wide gap semiconductors, polymers, etc. In some cases, a high quantum yield of not only exciton but also recombination luminescence is achieved[551].
It has been found that the presence of localized states reduces the exciton lifetime. Klimov[94] concurrently studied the dynamics of photoluminescence and transient absorption in CdSe QDs in TOPO with a femtosecond resolution. The author showed that charge carriers are trapped from the exciton state within about 1 ps. The enhancement of the impurity luminescence occurs over an exceptionally short time of 400 – 700 fs and is determined by the fast rate of trapping of the carriers. Logunov et al.[530], who studied the exciton decay dynamics using the pump – probe method found a red shift of the bleaching band of the exciton for short times of up to 2.5 ps; this was attributed to the relaxation of holes in the traps, since this process does not depend on the adsorption of electron acceptors. The adsorption of electron acceptors on QD interfaces revealed that the slow component in exciton dynamics is due to electrons. The time scale of hole capture dynamics is about 2.5 ps. The electron capture usually occurs at surface traps within 25 – 55 ps[94, 515, 531, 532, 552]. Later, it was shown for CdSe QDs that the transient bleaching band for 1Se – 1S3/2 is due to electron dynamics. To study the hole relaxation dynamics, it was proposed to examine the transient absorption on the red side of the 1Se – 1S3/2 bleaching band[94, 516, 533, 543].
For CdS QD, the same method revealed non-exponential dynamics of electron capture at localized states[475]. The characteristic time of the fast component was several picoseconds. In this case, the hole was captured within a sub-picosecond time, which determined the predominance of trap luminescence over exciton luminescence[475].
The progress in experimental studes of the exciton decay dynamics in Ag2S QDs is significantly more modest. The reasons for the absence of an allowed exciton absorption band in the stationary spectra are still a matter of discussion[147, 150, 353, 393]. It is assumed that Ag2S QDs do not exhibit exciton absorption features due to the indirect band gap[534]. At several wavelengths near the first harmonic wave of a Ti-sapphire laser (720, 790, 820 and 900 nm), a signal of transient absorption evolving into bleaching was observed. Later, the absence of exciton transitions in Ag2S QDs was recognized as a special electronic feature[392]. The use of the pump – probe technique in the spectral range from 520 to 730 nm for Ag2S QDs made it possible to detect a transient absorption signal that decayed within a few picoseconds[150]. For Ag2S QDs coated with thioglycolic acid molecules, a wide transient absorption band was discovered in the spectral range of 500 – 1000 nm; this band decayed according to a non-exponential law within a time of ≈ 1 ns[196]. It was found that the broad transient absorption band is determined by the capture of charge carriers by localized states of structural defect levels in Ag2S QDs. It was been shown that non-linear absorption can be effectively used in optical power limiting systems for 10 ns pulses.
An interesting result was reported by Gilmore et al[507]. It was found that upon direct excitation of localized states of PbS QDs, a bleaching band associated with traps is first formed at the long-wavelength exciton absorption edge; this is followed by the formation of a transient bleaching band in the exciton peak. Considering the ratio of the magnitudes of the induced bleaching signals in these two bands, the authors assumed that the trap absorption cross-section is 2 – 3 times greater than the similar value for exciton absorption.
Experimental data on the exciton decay time in PbS QDs are significantly different. For example, the decay time of exciton luminescence was reported[366, 553-555] to be approximately 1 – 2 μs. Meanwhile, other publications[556-558] report fast pico- to nanosecond dynamics of exciton decay in PbS QDs. However, according to Gilmore et al.[507], the bleaching peak related to the exciton ground state in QD PbS does not decay noticeably on a time scale of 2.5 ns. This suggests that the exciton decay is an order of magnitude slower. An ultrafast exciton decay was found for PbS quantum dots; the decay was due to the recombination of an exciton electron and a hole with a localized surface ion pair formed upon the adsorption of tetracyanoquinodimethane[559], the photoluminescence of PbS QDs being strongly quenched due to this process. It has been shown that the rate constant of the exciton excitation decay increases approximately linearly with increasing number of adsorbed acceptor molecules. It should be especially emphasized that the estimated exciton decay time obtained for PbS QDs untreated with acceptor molecules is 2.3 μs, which corresponds to the decay time of exciton luminescence for PbS QDs[366, 553-555].
In the case of PbSe QDs, it was found that the decay time of exciton luminescence is 880 ns[560]. This value correlates with the data obtained by Du et al.[561], who found the exciton radiation time to be 200 – 500 ns. It was assumed that such a long exciton lifetime is characteristic of all QDs made of Group 4 – 6 compounds with high optical dielectric constants[560].
According to an alternative point of view, the long time of radiative decay of the luminescence of PbSe quantum dots is determined primarily by the orbital nature of the edge single-particle wave functions, rather than by the electron – hole exchange splitting[562].
One more process that competes with exciton thermalization in QDs is multi-exciton generation (MEG). Upon excitation of a high-energy exciton with an energy exceeding the ground state exciton energy several-fold, the formation of several electron – hole pairs is likely due to the Auger process[535]. The possibility of optimizing MEG for efficient conversion of the energy of solar radiation photons, which accounts for the interest in the research in this area, has been assessed by several research teams using various QDs, including PbS, PbSe, CdSe, etc[535, 536]. In the photocurrent of QD-based solar cells, MEG exhibits an external quantum efficiency (the number of harvested electron – hole pairs referred to the number of incident photons) of about 114% with a threshold value of the quantum energy of 2.6 Eg[537]. The key process providing MEG is Auger shock ionization by a hot exciton, which, due to the greatly enhanced Coulomb interaction under quantum confinement, has a significantly higher probability than that in bulk semiconductors. Investigation of MEG in Ag2S QDs passivated with 3-mercaptopropionic acid[563] by pump – probe spectroscopy demonstrated that, regardless of the QD size, the lifetime of multi-excitons in Ag2S QDs is approximately 1 – 2 orders of magnitude longer than that in QDs PbS. Hence, Ag2S QDs is a promising candidate for solar cell applications. The transient absorption spectra under low-intensity excitation conditions were found to exhibit a bleaching band in the exciton absorption region, while the recovery dynamics showed that the exciton lifetime is on a nanosecond time scale. However, quantitative data on the exciton dynamics are also lacking[563]. A bleaching band in the range of 900 – 1100 nm of the transient absorption spectra was reported by Lin et al[538]. Despite the absence of an exciton structure in the stationary absorption spectra, this bleaching band was also interpreted as a band associated with the formation of an exciton. The excitation decay times were determined: the relaxation time of charge carrier thermalization was \( \tau_{th} = 40.9 \text{ps} \); the relaxation time for the Auger recombination was \( \tau_{au} = 27.9 \text{ps} \); and the relaxation time for exciton recombination was \( \tau_{re} = 3 \text{ns} \). The obtained exciton lifetimes do not take into account the non-radiative decay via recombination or capture of charge carriers and represent the lower limits of this quantity.
In conclusion, we would like to note the following. If nanosecond luminescence kinetics is used, it is necessary to bear in mind that the exciton ground state decays in two ways: (i) radiative annihilation of the exciton and (ii) trapping of charge carriers into localized states, including radiative (recombination luminescence centres) and non-radiative transitions. The decisive role of localized QD states in the excitation decay has been repeatedly emphasized[516, 517, 519, 523]. The decay kinetics of recombination luminescence is usually non-exponential. Some studies suggest a multiplicity of excitation decay channels that determine the law of luminescence decay[102, 108, 539]. For example, the complex law of luminescence decay (the sum of three exponents) reported by Katsaba et al.[102] was successfully attributed to the presence of three luminescence centres detected in the spectra. The temperature dependences of the luminescence intensity of these three bands are related in a complex manner and are determined by the relocalization of charge carriers between luminescence centres as the temperature changes. It was shown[564] that the approximation of the luminescence kinetics of QDs by two or three exponents has a clear physical meaning only in some situations, when a specific dynamic process can be attributed to each component. Usually, the variety of decay channels of excitations, taking into account localized states, cannot be detailed in the intricate law of luminescence decay. In the general case, when the luminescence quantum yield is noticeably lower than unity due to the non-radiative transfer of excitation energy from QDs to some external quencher (solvent molecule, oxygen molecule in solution, etc.), the decay kinetics for the dipole – dipole luminescence mechanism has the form[565]
where \( \tau_0 \) is the luminescence lifetime and \( t \) is time.
If the luminescence quencher (non-radiative recombination centre) is incorporated in QD, the number of centres in each QD of the ensemble is Poisson distributed, and the rate of energy transfer to one acceptor is constant \( k_q \), then the kinetics of the decay of donor luminescence is given by[566-570]
where \( m \) is the average number of quencher molecules per donor, \( \tau_D \) is the luminescence lifetime of the donor without a quencher, \( k_q \) is the quenching rate constant and \( t \) is time. In both cases, the law of luminescence decay in the presence of non-radiative energy transfer is non-exponential. Thus, taking into account the rate distribution of the electron and hole recombination in the sample provides for a non-exponential luminescence decay due to both the presence of luminescence quenchers and the distribution of distances between the QD electron and hole traps. Generally speaking, the rate constant distribution of any kinetic process for ensemble samples will lead to non-exponential kinetics of this process.
Thus, for QDs of many semiconductor compounds, including cadmium, zinc, and silver sulfides, there is still unsolved problem of identifying the stages and mechanisms of exciton decay, as well as the dynamics of recombination luminescence characteristic of non-stoichiometric colloidal QDs.
3.4. Temperature behaviour of spectral parameters
Detailed characterization of the optical properties of QDs is a key conditions for application of QDs for various purposes. Apart from the size effect, the band gap and the spectral kinetic properties of various optical transitions considered above are affected by the temperature of the environment. By investigating the influence of this factor, it is possible to derive information about fundamental characteristics such as the temperature coefficient \( \beta = \text{d}E_{g}/\text{d}T \), the effective phonon energy and the strength of the electron – phonon coupling. In the linear approximation, the temperature-induced change in the band gap is described by the model[571, 572]
According to this approach, the \( \beta \) value is determined from the slope of the linear segment of the experimental temperature dependence \( E_{g}(T) \). However, in the low-temperature region, it can be essentially non-linear.
The linear quadratic equation proposed by Varshni[573], which is widely used to describe \( E_{g}(T) \), has the form
where \( \alpha_1 \) and \( \alpha_2 \) are empirical parameters that have no particular physical meaning. The constant \( \alpha_2 \) is taken to be similar in magnitude to the Debye temperature. In the high-temperature limit where \( T \gg \alpha_2 \), it follows from Eqn (22) that \( \alpha_1 \approx \beta \). In some cases, coefficients \( \alpha_1 \) and \( \alpha_2 \) are negative, which complicates the physical interpretation of the measured dependences. Nevertheless, despite the limited amount of extracted information, the expression describes quite satisfactorily the experimental shape of the temperature characteristic \( E_{g}(T) \), which was verified for numerous examples[574].
In the framework of one-phonon approximation and second-order perturbation theory, the temperature dependence of the band gap can be represented as the equation[575-577]
where \( \langle n_s\rangle = [exp(\hbar \omega/kT ) – 1]^{–1} \). Here \( A_F \) is the Fan parameter depending on the microscopic properties of the material, eV; \( \langle n_s\rangle \) is the Bose – Einstein factor for phonons with the \( \hbar \omega \) energy; \( k \) is the Boltzmann constant, eV K–1. Previously[574], it was shown that in the high-temperature limit (\( kT \gg \hbar \omega \)), Eqn (23) is reduced to form (21), and then the temperature coefficient is expressed as
It is noteworthy that expression (23) does not explicitly take into account the contribution of the thermal expansion of the lattice. In the case of bulk materials, this contribution to the total temperature-induced change in the band gap is approximately 20%, and in the first approximation, it can be neglected[575, 578]. In addition, it can be taken that at high temperatures, the contribution of the thermal expansion to the shift of energy levels is also proportional to \( \langle n_s\rangle \)[578]. In this case, the calculated \( A_F \) value takes into account both the internal (electron – phonon coupling) and external (thermal expansion) contributions to the \( E_{g}(T) \) dependence.
The relationship between Varshni relation (22) and Fan expression (23) at \( kT \gg \hbar \omega \) was derived by Vainshtein et al.[575]
Hence, if the condition \( T \gg 2 \alpha_2 \) is met, the Varshni coefficients \( \alpha_1 \) and \( \alpha_2 \) should contain information on the effective energy of phonons.
A semiempirical relationship was proposed[579], explicitly taking into account both the expansion coefficient and the electron – phonon coupling
where \( U_1 \), \( U_2 \) and \( U_3 \) are temperature-independent parameters. The second term of the right-hand part of (26) is the temperature expansion and the third term is the electron – phonon coupling. It can be easily seen that the second and third terms in the right-hand parts of expressions (23) and (26), respectively, coincide, and \( A_F = 2U_{3} \hbar \omega \).
Experimental data were approximated[580, 581] using the expression
where \( a–z = E_{g}(0)\), \( z \) is the parameter characterizing the strength of the electron – phonon coupling. A comparison of expressions (23) and (27) indicates that \( A_F = 2z \).
For the description of the temperature dependence of the position of the exciton peak, Pässler et al.[582] used the model
where \( \chi \) is the limiting high-temperature slope of the dependence, and \( \Theta \) is the effective temperature of phonons. A comparison of expressions (23) and (28) shows that \( \chi = \beta_{\infty} \) .
O’Donnell and Chen[583] used the following relation to describe the temperature dependence of \( E_g \) for semiconductors
where \( S_{hr} \) is the Huang – Rhys parameter proportional to the strength of the electron – phonon coupling[584, 585]. A comparison of expressions (23) and (29) indicates that \( A_F = 2S_{hr}\hbar \omega \). Thus, it is obvious that expressions (23), (26), (27), (28) and (29) are analogous to one another; when they are used to describe the temperature dependences of \( E_g \) in materials, it is possible to calculate the effective energy of phonons. The presented models for \( E_{g}(T) \) have been traditionally used to describe the properties of bulk materials, but they are also employed for low-dimensional objects[581, 584-592].
In the general case, the positions of energy levels in quantum dots are affected by four temperature-dependent factors: thermal expansion of the lattice, thermal expansion of the envelope wave function, mechanical stress and electron – phonon coupling[572, 593]. The electron – phonon contribution predominates for both quantum dots[593] and bulk materials[574]. Therefore, it appears more substantiated to use models that explicitly take into account the phonon statistics and make it possible to extract information about the effective energy of phonons that determine the observed shifts of energy levels via interactions.
A temperature change influences not only \( E_g \) but also the half-width \( H \) of the corresponding optical components. For analysis of this value, it is very important that QDs feature size distribution and other distributions, which gives rise to inhomogeneous broadening under conditions of quantum confinement. Consider the behaviour of the half-width of single nanocrystal optical band \( w \), which can be represented in the following way for any temperature:
Here the first term reflects the natural line width at zero temperature, while the second one takes account of the effects leading to temperature-dependent broadening. In the framework of the exciton – phonon coupling, the contribution to the homogeneous broadening is defined as[584, 585, 594]
where \( \sigma \) is the exciton – acoustic phonon coupling coefficient, eV K–1; \( A_b \) reflects the strength of the exciton – LO phonon coupling with the \( \hbar \omega_b \) energy. In this case, the considered \( \Delta_w \) value quantitatively characterizes the dynamic disorder, which accounts for the temperature-dependent contribution to the energy level broadening caused by lattice vibrations.
In real systems, due to the scatter of QD characteristics, the first exciton peak energy differs for different nanocrystals in an ensemble[595]. Therefore, even at zero temperature, the half-width \( H \) of the exciton band for an ensemble is greater than \( w \) for separate nanocrystals, because it is formed by a set of closely located, overlapping peaks with different energies. In this case, the optical absorption band is inhomogeneously broadened, and \( \Delta_I \) quantitatively characterizes the static structural disorder, which provides the temperature-independent contribution to the broadening of energy levels[596, 597]. The static disorder is caused by distributions \( f(X) \) of other parameters \( X = \{x_1 , x_2 ,...\} \) for QDs in an ensemble. As the temperature increases, the bands for single nanocrystals are broadened according to Eqn (31), which, in turn, influences the \( H \) value for the exciton band of the whole ensemble, resulting in the temperature-dependent contribution \( \Delta_{T}(X,T) \) to the broadening. The temperature evolution of the half-width H of the nanocrystal ensemble with some distribution \( f \) can be represented in the form
In this case, broadening is determined by the effect of both static and dynamic types of structural disorder.
Expression (30) is widely used to analyze the half-width of the absorption bands of QD samples[577, 584, 585, 589, 591, 598, 599]. However, for analysis of H(T) dependences, it is necessary to consider the static structural disorder. The homogeneous broadening leads to the overlap of the spectral components of single nanocrystals to form the integral optical band of the QD ensemble. In this case, a reliable estimate of the exciton – phonon coupling parameters based on analysis of the temperature-dependent broadening of the optical spectra should include the possible contribution of inhomogeneous broadening factors[600].
The temperature has a considerable effect on the luminescence intensity of both bulk and zero-dimensional semiconductors. The traditional model for the temperature-dependent quenching of photoluminescence in solids, which takes into account the relationship between the probabilities of radiative and non-radiative transitions between discrete energy levels, can be represented by the known Mott expression[601-605].
where the function \( \eta(T,E_q) \) describes the efficiency of radiative transitions; \( I_0 \) is the luminescence intensity without quenching, rel.u.; \( p \) is the dimensionless pre-exponential factor; \( E_q \) is the activation energy of quenching, eV. When the quenching mechanism involves several non-radiative relaxation channels, additional temperature terms with parameters \( p \) and \( E_q \) appear in the efficiency function[606-612]. In the case of QD ensembles characterized by a scatter of structural parameters and the corresponding energy levels, the temperature dependence of PL intensity can be written with allowance for the distribution of the quenching activation energy \( f(E_q) \) [613].
The distribution of the activation energy was previously successfully used for analysis of the temperature-dependent quenching of photoluminescence for amorphous a-SiO2 and a-Si : H[614-616], lead silicate glasses and disordered systems of various natures[617-619].
Thus, the effect of temperature on the optical absorption and photoluminescence spectra is manifested as a shift of maxima and a change in the band half-width and also the temperature-dependent luminescence quenching. In the case of InP/ZnS nanocrystals, a temperature rise in the 300 – 525 K range induces a red shift and broadening of the PL bands[584]. The temperature-dependent change in \( E_{q}^{eff} \) was described in the framework of the model equations (22) and (29). The results of data approximation according to the Varshni expression are consistent with the values for bulk InP. The analysis showed that the electron – phonon coupling increases with decreasing QD diameter, with the phonon energy being in the range of 8 – 19 meV. These values are much lower than the energy of longitudinal (LO) and transverse (TO) optical vibrational modes for the case of bulk crystal and are consistent with the longitudinal acoustic (LA) modes. Analysis of the temperature-dependent broadening of the luminescence band reveals an influence of optical phonons with 40 meV energy; however, the predominant contribution is attributed to acoustic vibrations. Analysis in a wider temperature range from 2 to 510 K led to similar conclusions about the mechanisms involved in the observed phenomena[585].
Study of the temperature dependence of the optical absorption of InP/ZnS showed that cooling from 296 to 6.5 K induces a blue shift of the first exciton band (Figure 13a). The temperature behaviour of the energy of the band maximum for QD ensemble is due to the increase in the QD energy gap and is adequately described by Eqn (23) (Figure 13b). It was found that the shift is due to the exciton – phonon coupling with the longitudinal acoustic modes characterized by energy in the 14 – 31 meV range and is consistent with the mechanisms of analogous processes in bulk indium phosphide crystals[377, 620].
It was also found for InP/ZnS that the half-width \( H \) of the first exciton absorption band does not change with temperature, being in the range of 227 – 375 meV for various QD samples[600, 620]. Numerical modelling demonstrated that the observed effect is due to the inhomogeneous broadening caused by the predominant contribution of the static structural disorder, which is related to the nanocrysral size distribution (Figure 14).
The temperature dependence of the PL spectra of closely packed InP/ZnS nanocrystals in the 15 – 300 K range was analyzed by Pham et al[621]. They noted that luminescence is formed by two bands with maxima at 2.06 and 1.8 eV, which were assigned to the exciton and defect-related transitions. The intensity of the low-energy component was maximum at low temperature and decreased with temperature rise up to room temperature. Simultaneously, the bands shifted to lower energy. The numerical description was carried out in the framework of the Varshni model, and the resulting parameters were close to the corresponding values for bulk InP. The presence of defects in InP/ZnS QDs was noted by Shirazi et al[622]. Using time-resolved measurements at different temperatures, the dynamics of recombination processes of an ensemble of nanocrystals was investigated. When T = 280 K, the decay kinetics is well described by three exponential components. On cooling below 140 K, the fourth component related to Auger recombination appears. The temperature evolution of the decay rate constants was explained using the four-level model including the levels of dark exciton, surface defect, bright exciton and a defect at the core/shell interface.
The model of exciton fine structure in QDs describing the degeneracy and splitting of the ground state into optically active (bright) and passive (dark) levels was first proposed for description of the properties of the CdSe nanocrystals[56, 93], but it was also used to interpret the observed optical phenomena for InP[623, 624]. Biadala et al.[625] also resorted to this concept for interpretation of the features of InP/ZnS QD luminescence. They studied several samples with InP core diameter from 2.4 to 3.3 nm and a shell thickness of approximately 2 nm exhibiting luminescence in the 2.45 to 1.9 eV range. As T decreased, low-energy bands located at approximately 300 meV distance from the maximum appeared in the spectra, with their intensity decreasing with increasing QD size. This emission was assigned to deep traps. Also, a shift of PL maximum to higher energy was observed, which was described by the Varshni relation with \( E_{g}^{eff}(0) = 2.019 \text{eV} \), \( \alpha_1 = 5.8 \times 10^{–4} \text{eV} \text{K}^{–1} \) and \( \alpha_2 = 320 \text{K} \). Study of the temperature-dependent PL decay kinetics showed that the observed features are caused by processes involving bright (allowed) and dark (spin-forbidden) states. The energy gap between these two lower exciton levels decreases from 16 to 5 meV with increasing size of the core. Also, an upper bright level located in the range from 40 to 147 meV above the doublet of the bright and dark states was observed in the fine structure.
The temperature dependence of the properties of CdTe QDs was found[626] to be essentially determined by the choice of precursors for their synthesis, their molar ratio, stabilizing ligands and particular conditions of synthesis. For all samples, a temperature rise from 298 to 348 K was accompanied by a red shift of the spectral maximum by 4 – 6 nm and a decrease in the luminescence intensity. As the samples were cooled to room temperature, the initial intensity was not restored, that is, static quenching took place, and the intensity continued to decrease with every new cycle. The irreversible quenching is related to the detachment of ligands from the QD surface, which resulted in a greater number of defects that serve as a non-radiative relaxation channel[627].
Most of materials obey a negative temperature dependence of \( E_g \) however, this is not always true. An opposite situation is observed, for example, for PbS and PbSe QDs[577, 598]. Study of the PL spectra of these QDs in the temperature range of 5 – 520 K showed that the energy and half-width of the exciton band increase with increasing T. At temperatures below 220 K, these dependences are adequately described by relations (22), (29) and (30); however, at higher T considerable deviations are observed. They are attributed to splitting of the ground level into dark and bright exciton states. The PL intensity decreases fivefold on heating in the range of 10 – 300 K[598].
The red shift of the PL maximum and increase in H as the temperature is raised from 80 to 500 K are also typical of CdSe/ZnS nanocrystals[628]. The former change is attributed to a decrease in the energy gap, while the latter one is due to the coupling with acoustic and LO phonons. Analysis of the change in the luminescence intensity with temperature provides the conclusion that quenching occurs via thermal escape of holes over the whole temperature range. At temperatures above 320 K, one more mechanism associated with the appearance of thermally induced defects is added. These defects lead to trapping of charge carriers on the surface followed by their non-radiative relaxation.
Singh et al.[629] investigated the photostability of some CdSe/CdS QD samples with different shell thicknesses. It was found that as a definite thickness is attained, the efficiency of recombination involving defective states markedly decreases, while the photostability under UV irradiation increases. The temperature dependence of the photoluminescence spectra in the range from 283 to 363 K also attests to an enhanced stability of nanocrystals of more than 8.5 nm in diameter with a thick shell, as PL quenching for these samples is virtually absent.
Li et al.[630] proposed a method for the synthesis of InP/ZnSe/ZnS QDs with a PL quantum yield close to unity at room temperature. The synthesis was performed using ZnF2 and, hence, the formation of an oxide layer on the InP surface was avoided, which provided a uniform building-up of the shell. On heating to 428 K, PL quenching was observed, and consequently the intensity decreased by 50%. The obtained samples had an enhanced thermal stability compared with analogous QDs synthesized using HF for which heating to the indicated temperature resulted in a decrease in the intensity by more than 90%.
The effect of shell thickness on the thermal stability of exciton PL was also demonstrated in relation to InP/ZnS QDs[613, 620]. Analysis of the exciton luminescence quenching in the range of 6.5 – 296 K showed that it occurs via thermally activated electron escape from the InP core into the ZnS shell. An increase in the shell thickness leads to a decrease in the energy of this barrier and increases the temperature stability of the QD PL. The shape of the temperature dependence of the luminescence intensity is described using the Gaussian distribution of the barrier energy caused by the scatter of parameters of separate nanocrystals in an ensemble (34). Quenching of defect-related InP/ZnS luminescence observed at temperatures below 100 K due to optically active centres based on indium and phosphorus dangling bonds at the core/shell interface was analyzed. It is also characterized by a barrier energy distribution and is formed, most of all, by the transitions of charge carriers from the acceptor defect levels to the ground states.
Thus, the equations proposed for bulk semiconductors describe quite successfully the temperature effects observed in QDs based on various semiconductor compounds: the shift and broadening of optical bands and photoluminescence quenching. The mechanisms of these effects, however, can be considerably modified due to specific features inherent in zero-dimensional systems. First of all, as has already been discussed, detailed analysis of the energy structure is required for each material, because the relative positions and energy of the levels depend on the size, shape, composition, crystal structure, defects, passivators, etc. Enhancement of the exchange interaction removes degeneracy of the levels and gives rise to dark and bright exciton states, which have a considerable effect on the relaxation processes. Taking account of the size distribution and distributions of other QD characteristics in an ensemble is also important, as it is necessary for reliable estimation of the exciton–phonon coupling parameters and for analysis of temperature-dependent quenching mechanisms of both exciton and defect-related luminescence of quantum dots.
3.5. Photonics of single quantum dots
Since the advent of the single-molecule spectroscopy more than thirty years ago (see paper by Orrit et al.[631] and references cited therein), which eliminated the undesirable averaging over an ensemble of emitters, the demand for this method and the scope of its application in various interdisciplinary fields have immensely enhanced. The detection of single emitters using an optical microscope is based on the requirement that at each instant of time, only one emitter operates within a diffraction-limited area. This can be achieved by reducing the concentration of single emitters or by targeted (selective) excitation of single emitters[632] and their photoactivation/deactivation[633]. In the latter case, a large number of single emitters can be resolved within a diffraction-limited area. This option has found application in super-resolution luminescence microscopy, enabling one to overcome the diffraction limit by tens of times. An equally important factor determining the possibility of detecting a single emitter is the high signal-to-noise ratio: autofluorescence of the environment in which the emitter is located and the detector noise may preclude the possibility of detecting a single emitter. The progress in the design of low-noise, highly efficient detectors (quantum efficiency QE > 95%) based on silicon structures has resulted in a significant increase in the efficiency of detecting weak luminescence signals from single emitters.
The research of quantum dots at the level of single emitters, which started in the mid-1990s (e.g., Grundmann et al.[634]), was aimed at elucidation of photochemical, photophysical and spectral phenomena that were not revealed in conventional studies due to ensemble averaging. The luminescence signal of single quantum dots can provide observation of luminescence blinking[635], photon antibunching[636], spectral diffusion[637, 638] and blinking of the delayed luminescence component[639], which reflect both the processes occurring inside the quantum dot and the interaction of quantum dots with a unique local environment.
The interest in the studies of single quantum dots is also associated with the potential possibility of using them as nanoscale probes for measuring local temperature[640], viscosity coefficient, pressure and refractive index of an optical medium[641]. In addition, single quantum dots are of interest for creating sources that emit strictly single photons on demand[642].
3.5.1. Photoluminescence blinking
An early study of single colloidal quantum dots carried out in 1996[635] gave a completely unexpected result: the luminescence of quantum dots under continuous photoexcitation underwent sharp abrupt changes in intensity. These transitions between high-intensity (on-state) and low-intensity (off-state) luminescence states occurred at random times. Figure 15a shows an example of time dependence of the luminescence signal of a single CdSe/ZnS quantum dot, demonstrating the blinking nature of luminescence. A similar blinking phenomenon was well known by that time for single molecules, in which the transition of an electron from an excited singlet to a triplet state, forbidden by selection rules, gave rise to dark gaps in the luminescence signal, while the reverse triplet-to-singlet transition led to the restoration of the luminescence signal.
To explain blinking, Efros and Rosen proposed a charging model[643], in which the dark off-state was attributed to the presence of an uncompensated charge inside the quantum dot. This charge generates a fast non-radiative recombination channel for electron – hole pairs related to the Auger mechanism, i.e., quenching of luminescence. Figure 15a presents the main idea of the charging model: radiative recombination of an electron – hole pair in the neutral QD state corresponds to on-state luminescence with a high quantum yield (Figure 15a, left), while predominantly non-radiative recombination by energy transfer to a third particle in the charged state of the quantum dot based on the Auger mechanism is an off-state with a low quantum yield (Figure 15a, right). The transition between states was attributed to discharging and charging of the quantum dot. Later, it was discovered that the distribution of times of on- and off-states is described by a power law[644], rather than by an exponential law, which can be explained by fluctuations in the probability of ionization and neutralization of a single quantum dot. This led to the development of a number of modified models based on the Auger mechanism of luminescence quenching in quantum dots[644-647].
In addition, it was found that blinking can have several intensity levels: in addition to the on- and off-states, an intermediate ‘grey’ state is also observed[648]. Finally, there are situations where the signal fluctuates between a quasi-continuous distribution of intensity levels[649]. Figure 15b (bottom) shows an example of such a luminescence trajectory.
An alternative mechanism explaining the luminescence quenching in quantum dots and blinking was proposed by Frantsuzov et al[650]. The luminescence quenching was explained by non-radiative transitions through charge carrier trapping by deep defect levels inside the band gap, while blinking was explained by a variation of the total rate of non-radiative recombination as a result of a change in the number of defect states over time (Figure 15b). One of the advantages of this model is that it can explain blinking with a large number of luminescence intensity levels.
To date, a large number of blinking models have been proposed, in which luminescence quenching is driven by the Auger or the trap mechanism[651-654]. Recent studies have shown that the blinking process can be due a few luminescence quenching mechanisms operating in parallel[647, 655, 656].
In addition to the luminescent signal with a characteristic decay time of ≈ 20 ns (in the on-state), the ensemble of quantum dots exhibits a weak component, the decay of which occurs in a time range up to tens of milliseconds[653, 654, 657, 658]. The appearance of this component (delayed luminescence) is attributed to the presence of shallow defect levels, the temporary trapping of charge carriers on which generates delayed luminescence photons, and to the effect of an external electrostatic field. Delayed luminescence was found for both the ensembles and single quantum dots. It is important that the kinetics of the slow component decay follows a power-law dependence on time, which correlates with the power-law distribution of the times of on- and off-states in the blinking of quantum dots. This experimental fact has initiated attempts to develop phenomenological models linking these two phenomena and explaining the power-law behaviour of both of them[653, 654]. Recently[639], it was shown that the delayed component of luminescence in single quantum dots undergoes fluctuations, on a macroscopic time scale, similar in nature to blinking of the fast luminescence component. However, blinking of delayed luminescence occurs independently of blinking of the fast component (luminescence) of quantum dots, which suggests that blinking of these two components is driven by different mechanisms. It should be noted that studying the mechanisms of luminescence blinking and quenching is important both for the design of non-blinking quantum dots and for the synthesis of quantum dots with controlled blinking. The former is necessary to enhance the quantum yield and photostability of QDs, which is required for the development of stable and efficient QD-based devices: photodiodes, displays, solar cells, and sources of non-classical radiation. The latter is needed for the development of photoswitchable fluorescent markers for super-resolution microscopy using QDs. Finally, it is necessary to gain an understanding of the nature of delayed luminescence as a phenomenon that significantly increases the excited state lifetime in quantum dots. This is required, in particular, for the design of fast-operating QD-based devices in which the time of switching between the excited and ground states limits the maximum operating rate.
3.5.2. Photon antibunching
The antibunching of photons is characteristic of a wide class of emitters, including single atoms, molecules, colour centres in crystals, semiconductor quantum dots, etc[636, 659-662]. The antibunching (anticorrelation) in a sequence of emitted photons is observed in the case when two or more photons cannot be emitted by a source simultaneously. This type of emission is described by sub-Poisson statistics, in which the dispersion of the number of photons is less than the mean value, which corresponds to a negative Mandel Q-parameter: Q < 0. The sources of non-classical radiation (single photon sources) are the basis for the implementation of a number of algorithms in quantum cryptography, which attracts a lot of attention to such sources. Most often, the Hanburry Brown and Twiss intensity interferometer is used to study the photon antibunching. In this experiment, the signal is divided between two single photon detectors and the number of coincidences separated by certain time delays is measured (as shown schematically in Figure 16a). The distribution of time intervals obtained in this way is a second-order cross-correlation function \( g^{(2)}(\tau) \) (under certain assumptions that are usually implemented in experiments with single emitters). In this distribution, a dip is observed near zero delay times \( g^{(2)}(0) \sim 0 \) (antibunching) for a source of single photons. An example of a \( g^{(2)}(\tau) \) function measured under pulsed excitation for a single quantum dot is shown in Figure 16b. It can be seen that in this case, there is no peak near zero delays \( g^{(2)}(0) \sim 0 \) responsible for the simultaneous emission of two or more photons. The measurements of photon antibunching are often used as an auxiliary study to confirm that the emitter is a single object, but also as an effective tool for studying the photophysics and photochemistry of various emitters, including organic molecules, quantum dots, semiconductor nano- and submicron crystals[656, 663-667]. In quantum dots, the emergence of antibunching is associated with fast non-radiative Auger recombination[636], which leads to the quenching of multi-exciton states and, consequently, the simultaneous emission of more than one photon becomes impossible. However, if the Auger ionization is suppressed, antibunching may not be observed or observed partially[664, 665]. A similar behaviour is inherent in quantum dots with multilayer shells characterized by radial variation of the ratio between the components, for example, between sulfur and selenium in CdSexS1–x, as shown by Park et al[656]. In this case, the probability of Auger recombination may significantly decrease due to the formation of a smooth potential of the quantum dot[668]. Understanding the photophysical processes occurring during multi-exciton excitation is important for the development of lasers based on quantum dots, where a high quantum yield of biexciton luminescence is required to implement an population inversion[656, 665]. Measuring \( g^{(2)}(0) \) makes it possible to estimate the ratio of the quantum yields of biexciton to exciton luminescence, \( g^{(2)}(0) = \eta_{bx}/\eta_{x} \), in quantum dots[664] (as shown schematically in Figure 16c) and the rate of non-radiative Auger recombination. Therefore, the examination of photoluminescence statistics is of fundamental importance in the study of the recombination dynamics of multi-exciton excitations and determination of the influence of structure and chemical composition on the possibility of obtaining quantum dots promising as stable sources of single photons, where a low quantum yield of biexciton luminescence is required, and as laser active media with a low lasing threshold, which, on the contrary, requires a high quantum yield of biexciton luminescence.
3.5.3. Spectral diffusion
Spectral diffusion is a random variation of the position of the spectral line of a single emitter over time. The dynamics of this process is observed in experiments with a sufficiently high time resolution, while at long exposures it can lead to a significant broadening of the observed luminescence spectral contour. The spectral diffusion can be manifested as discrete jumps of the spectral line between several positions, which is typical of low-temperature spectra of single molecules embedded in a high-molecular-weight polymer and interacting with tunnelling two-level systems (Figure 17a). Also, low-temperature spectral diffusion can occur as a random drift in the position of the spectral line, which is observed, for example, for single molecules embedded in organic glass or a low-molecular-weight polymer at cryogenic temperatures (Figure 17b)[669].
Bawendi and co-workers[670] were the first to observe the spectral diffusion in colloidal quantum dots. The authors showed that the luminescence spectra of single CdSe quantum dots at a temperature of 10 K consist of two peaks corresponding to an electronic transition (phononless line) and a repetition associated with transitions giving an optical phonon (LO phonon) and shifted to the red region of the spectrum. The discovered structure of the spectrum was close to the results obtained by ensemble measurements; however, in the case of single quantum dots, the linewidth was more than 50 times narrower. In addition, the position of the luminescence spectrum underwent random shifts in time by up to 60 meV, in which a correlation was observed between the magnitude of the shift and the change in the coupling with the LO phonon. Later, it was shown[671] that application of an external field also leads to a similar shift in the luminescence spectra of single quantum dots and LO phonon coupling changing. This suggested a relationship between the spectral diffusion and the variation of local electric field via the quantum-confined Stark effect (QCSE). This idea was further developed by Neuhauser et al.[672], who investigated the relationship between luminescence blinking and spectral diffusion. A correlation was found between events of transition to the on-state and large spectral jumps. The correlation was explained by the ionization dynamics of electrons and holes in the quantum dot, which results in the simultaneous change in the total charge delocalized inside QD and the configuration of the charge localized on the QD surface. According to the proposed concept, the former should lead to blinking (charging model), while the latter should induce a local field variation and a change in the exciton energy due to QCSE. The idea that spectral diffusion is associated with a change in the charge localized on the QD surface has been used to explain the correlation between the linewidth and luminescence peak position in CdSe quantum dots coated with asymmetrical CdS shells[673]. The authors hypothesized that the simultaneous shift and broadening of the spectra are associated with the movement and oscillation of charges on the shell surface, it is due to the average local field and its’ modulation in the QD core change in a correlated manner as the charge moves along the elongated shell.
However, this hypothesis was questioned by subsequent studies, which found a similar correlation between the position and width of the luminescence spectrum measured at room temperature for symmetrical CdSe/CdS/ZnS quantum dots[674]. Moreover, the distribution of spectral shifts characterizing the scale of spectral diffusion did not depend on the dielectric constant of the polymer matrix surrounding the quantum dots, which led to the conclusion that spectral diffusion in quantum dots is not related to surface charges, but is driven by internal processes.
Finally, a linear correlation was also found[638] between the width and position of the luminescence peak for symmetrical CdSeS/ZnS quantum dots. A model providing a quantitative description of the experimentally observed dependences was proposed. In this model, the simultaneous change in the width and position of the spectral line was explained by variation of the electron – phonon coupling[638, 651]. Figure 18 shows an example of the spectral diffusion of a single CdSeS/ZnS QD at room temperature (Figure 18a) and the correlation between the width and position of the luminescence spectral line (Figure 18b).
3.5.4. Raman spectra of single QDs
Modern experimental techniques make it possible to record Raman spectra of both an ensemble of QDs (Figure 19a)[675] and a single QD (Figure 19b)[676].In the case of single QD, it is necessary to attain a significant increase in the process cross-section; this is done by using the surface enhanced Raman scattering (SERS) or tip enhanced Raman scattering (TERS) effects[676]. In these experiments, specific features associated with the QD size (phonon confinement, surface phonons) can be analyzed, along with more complex size effects for ultra-small nanocrystals associated with the activation of the phonon density of states changed by surface reconstruction. Actually, this technique enables direct measurement of the spectrum of localized phonons. Analysis of phonon spectra is used to quantify core and shell stresses and the degree of interface mixing and to monitor surface oxidation.
Thus, studies of single QDs make it possible to reveal completely new unique phenomena that are masked by averaging over an ensemble of particles in conventional spectroscopic studies. These features are also promising for practical applications. In particular, photostability and high luminescence quantum yield have become the basis for QD applications in optoelectronics, while the high sensitivity of the optical and spectral characteristics of QDs to external parameters enables them to be used as spectral nanoprobes.
The possibility of using quantum dots to address applied problems largely depends on physical characteristics such as luminescence quantum yield, photostability, quantum yield of biexciton luminescence, delayed luminescence, etc. The understanding of the microscopic nature of photophysical processes can significantly facilitate the design of of quantum dots with desired properties needed for various applications.
3.5.5. Fluorescence nanoscopy of single QDs
Fluorescence images of single QDs can be recorded using a highly sensitive one- or two-dimensional detector by means of a confocal scanning or a wide-field epiluminescence microscope, respectively. Figure 20 shows examples of four sequentially recorded fluorescent images of single colloidal CdSeS/ZnS QDs in a microscope field of view measuring 20 × 20 μm2 deposited on a glass substrate at room temperature[677].
The sizes of fluorescence images \( \sigma_{\mathrm{PSF}} \) of single point sources (in our case, single quantum dots, see an example in Figure 21a) are determined by the diffraction of light on the microscope optical parts and depend primarily on the numerical aperture of the microlens \( NA \): \( \sigma_{\mathrm{PSF}}=\frac{\lambda_m}{2NA} \)
where \( \lambda_m \) is the luminescence wavelength, and PSF is the point spread function. Point sources are those sources the dimensions of which are significantly smaller than their luminescence wavelength. In this case, the accuracy of the reconstructed transverse QD coordinates \( \sigma_{X,Y} \) found by the mathematical processing of the image (for example, by approximating the image with a two-dimensional Gaussian function) can be significantly higher than the diffraction limitation. In the simplest terms, the accuracy \( \sigma_{X,Y} \) is determined by the width of the point spread function \( \sigma_{\mathrm{PSF}} \) and the number of measured photons \( N \), forming an image of a point source \( \sigma_{X,Y}=\frac{\sigma_{\mathrm{PSF}}}{N^{1 / 2}} \)
A more accurate formula takes into account the image discreteness (the relationship between the PSF size and the spatial sampling step) and the presence of spurious noise[678]
where \( \xi \) is the pixel size of the CCD camera, and \( \varphi \) is the noise level (light contamination).
Figure 21b shows an example of the distribution of the reconstructed lateral coordinate of the luminescence centre of a single CdSe/ZnS quantum dot with a luminescence wavelength of ~ 600 nm upon successive processing of a large number of images (the process is shown schematically in Figure 21a). The accuracy of determining the coordinates can be estimated from the resulting spread of \( X, Y \) values. Figure 21c shows the accuracy of reconstruction of the transverse coordinates \( \sigma_{X,Y} \) of single QD (with emitting core of 4.2 nm size) as a function of the total number of collected photons \( N \) forming each image. The dependence is a power function with an exponent of about –0.5. The pattern of this dependence is retained for accuracy levels comparable to and smaller than the size of the QD core in which the electron – hole pair is delocalized and undergoes radiative recombination. With a sufficiently long acquisition time (seconds or longer), the accuracy of coordinate reconstruction can be higher than 0.5 nm, which is approximately 10 times smaller than the core size of single QD[677]. This can potentially be used for precision studies of recombination processes in quantum dots under variation of external parameters.
The possibility of reconstructing the coordinates of single QDs with a subdiffraction accuracy can be used for optical nanotracking (detection of nanometre motions) of single quantum dots. Figure 21d shows an example of optical nanotracking of a CdSe/ZnS quantum dot, which was shifted in a controlled manner in the focal plane of the microscope with nanometre precision using a piezoscanner (the measurement was made by analogy with the studies reported by Eremchev et al.[677]). Each cloud of points in this plot represents the reconstructed coordinates of a single quantum dot at a fixed position of the piezoscanner. It can be seen that in this case, displacements over distances of ~20 nm can be resolved with high reliability. It should be noted that nanotracking of quantum dots can also be carried out in 3D space[679]using specially designed diffractive optical elements and rotating light-field technique.
To implement full-fledged luminescence nanoscopy within each diffraction-limited region, it is necessary to resolve a large number of point sources. Naturally, these sources should be spatially connected with the object under study, for example, they should be located on its surface. This approach can be implemented making use of the photoluminescence blinking effect[680, 681], in which quantum dots switch between on- and off-states. In this case, QDs do not emit simultaneously and can, in principle, be detected separately. A similar approach was used to determine the distance between two quantum dots[681], with this distance being smaller than the luminescence wavelength. In addition, a very simple selection of luminescence based on the QD emission wavelength also makes it possible to use QDs as markers in the localization nanoscopy technique. Currently, QDs are used for imaging of biological objects with ultrahigh spatial resolution[682].
4. Some applications of quantum dots
4.1. Biology and medicine
Over the period of time that passed since the beginning of the synthesis and study of QDs, not only new synthetic procedures have been successfully developed, but also various practical applications of QDs have been proposed. In particular, considerable attention is given to issues related to the diagnosis and treatment of human diseases and applications in biology. There are methods for QD incubation with endothelial and stem cells followed by non-invasive monitoring of their pathways in tissues, fluorescence immunoassay, targeted delivery and prolonged release of drugs and genes, cancer diagnosis and therapy, visualization and treatment of other diseases; combinations of QDs with magnetic particles are used for the targeted delivery and therapy[683-687].
The idea of using QDs for imaging is directly related to their physicochemical properties, chemical stability, photostability, size dependence of the luminescence range and possibility of exciting QDs of different sizes using a single radiation source. Owing to these properties, QDs can compete with organic dyes, which are widely used in biology and medicine. Organic dyes do not possess photostability; each dye has a particular emission range and requires excitation at a definite wavelength, which complicates simultaneous observation of several objects. Furthermore, the preparation of assay kits is complicated, ready specimens require special storage conditions and cannot be stored for long.
The use of QDs as donors is based on stimulated luminescence of acceptors (for example, organic molecules) in the presence of QDs and has been theoretically substantiated by V.M.Agranovich and co-workers[688, 689].
In the case of the weak bonding of excitons in a semiconductor and in organic compounds where the width of the corresponding levels is greater than the resonance interaction energy, which is true for most organic compounds, incoherent non-radiative energy transfer from the donor to the acceptor, i.e., the Förster resonance energy transfer, takes place[690]. In this case, QD is the donor and an organic molecule is the acceptor. For effective energy transfer, the distance from the donor to the acceptor should be 2 to 5 nm. If the time of energy transfer from QD to an organic compound is shorter than or equal to the Wannier – Mott exciton lifetime, a significant part of energy from the excited QD can pass to the organic compounds. The general procedure for energy calculation in the hybrid nanostructure[691] was applied to determine the Förster energy transfer rate. The calculation of the Joule loss for the electric field generated by the excitonic polarization of QD in an organic medium showed that the transfer time is approximately 20 ps, which is significantly shorter than the exciton lifetime in QDs[689]. However, in some hybrid configurations, not only energy transfer but also charge carrier transfer can take place, which may change the phase composition of QDs and change the aggregative stability of colloids[692, 693]. On the other hand, charge transfer enables the use of QDs for photocatalysis.
Colloidal quantum dots are used most often in biology and medicine, because they can be inserted into living cells or tissues. The implementation of these methods requires non-toxic, bioinert or bioactive materials. Therefore, of most importance is the toxicity of compounds used to obtain QDs, including the solvent and stabilizer that functionalize the surface of molecules and semiconductor core. The use of organic solvents to produce colloids allows better control over the size and shape of QDs. Quantum dots obtained in toxic organic solvents exhibit intense luminescence, but they require long-term complex preparation for the use in a living cell or a living body and a special protocol for each type of objects. An alternative is the use of bioinert water. The existing difficulties of attaining the desired physicochemical properties are gradually overcome when water is used, and nowadays water-soluble QDs compete with those obtained in organic liquids[301, 694]. The use of bioinert or bioactive organic molecules for stabilization of semiconductor QDs is a prospective strategy, which, together with stabilization, solves the problems of environmental protection from the possible toxic effects of the core and functionalizes QDs for the subsequent use. By selection of the ligand, it is possible to affect the size, shape, interaction with proteins, circulation in the body and drug transfer[695, 696] and to develop methods for selective cell treatment[697]. Specific surface modification is also necessary for target-based drug screening and real-time active biosensing of cellular processes[698].
The studies directed towards the practical use in vivo are related, first of all, to QDs that show luminescence at the boundary between red and infrared and in the near-infrared spectral region, i.e., in the range from 650 to 1200 nm. This interest is based on deep penetration of this radiation into living tissues and high signal-to-noise ratio, which allows successful use of these QDs for imaging, photoablation and photodynamic therapy[699, 700]. Near-IR light penetrates through 10 cm of breast tissue and 4 cm of skull tissue when a few-microwatt sources are used[701]. The radiation absorption or scattering is determined by the properties of irradiated tissues. Scattering depends on the composition and morphology of particular body tissue, while haemoglobin, melamine and water absorb radiation in this frequency range[702-704]. Thus, the local distribution of body tissues can control the energy distribution and set the boundaries for IR-activated drug release. These factors are taken into account for the development of targeted drug delivery to minimize the adverse side effects in the treatment of inoperable cancer. A recent achievement in this field is appearance of theranostics[705, 706]. According to this method, remarkable optical properties, broad absorption range and anticancer activity of silver sulfide (Ag2S)-based QDs are used simultaneously for imaging and hyperthermia of cancer cells[707, 708].
The whole range of issues related to toxicity attracts considerable attention of both the researchers who develop particular applications and those who explore the general issues[709-711]. Resent studies have proved that toxicity cannot be determined by a single parameter, but depends on numerous factors. Oh et al.[712] showed that these factors include QD concentration, size and surface properties, shell composition, functionalizing compounds and residence time in a biological medium[695, 713, 714]. Positively charged particles are more likely to be toxic, while negatively charged particles would rather have low toxicity[715]. For example, the toxicity of cadmium-containing QDs was initially attributed to the release of cadmium ions. The latest cytotoxicity assays for CdS QDs in vitro using various cell cultures demonstrated that aqueous colloidal solutions have moderate toxicity caused by the remainders of precursors used for the synthesis (Figure 22)[716].
After washing with acetone and redissolution, the index of cytotoxicity (IC) of CdS QDs decreased to 15 – 18% depending on the concentration, which gave low-toxic aqueous colloidal solutions of CdS QDs with concentrations of 2 to 8 mM.
Quantum dots can penetrate into cells and be accumulated in tissues. On the one hand, this makes them applicable for therapy when they are accumulated in the branched vascular network formed in a cancerous tumour. On the other hand, uncontrolled penetration and accumulation can cause damage to both the body and the environment. The mechanism of penetration into the cell has not been ultimately clarified. Particular mechanisms for the cellular uptake of QDs include phagocytosis, pinocytosis and receptor- or caveolin-mediated endocytosis, with the choice depending on both the cell and particle characteristics. The mechanism can be either passive or active depending on the size and surface properties (Figure 23)[717]. According to some data, the renal filtration threshold for QDs is 6 – 8 nm, but attached ligands increase the hydrodynamic diameter and allow blood circulation of QDs[718, 719]. Some other data indicate that nanoparticles coated by special organic ligands, with a total size of 39 nm, are able to penetrate into the cell nucleus through the nuclear pore[720].
Although the unsolved issues of QD toxicity retard their use in vivo, the development of in vitro studies continues apace. In this case, it is necessary to take into account the QD charge and size and the concentration of colloidal solutions[695, 721, 722]. Several stages of QD interaction with the cells were detected. In the first stage, QDs are accumulated on the cell membrane, and then they subsequently penetrate into the cytoplasm and the nucleus[714]. The degree of uptake depends on the time of conjugation and cell type, functional state and activity. The time needed for QD penetration into cells and nucleus may range from 15 min to two hours. The development of personalized medicine requires new diagnostic methods without labour-intensive sample preparation processes or the use of expensive equipment. One of such methods is the fluorescence immunoassay. As an example, the efficacy of using aqueous colloidal solutions of CdS QDs for fluorescence diagnosis of herpes infection was demonstrated in relation to human cytomegalovirus (CMV). The LECh-3 diploid cells (Cell Culture Laboratory of the Ekaterinburg Research Institute of Viral Infections) were infected with this virus (reference strain AD169, titer 5.0 lg, tissue cytopathogenic dose of 50 mL–1)[723]. The test specimens for fluorescence microscopy were prepared for healthy cells 24, 48 and 72 h after introduction of infection by adding CdS QDs into test tubes containing monolayers of infected cells on a cover glass. After 60 min, the glasses were taken out and dried at room temperature. Intact culture samples incubated with QDs and infected cells at all stages without QDs were used as controls. The results of cell examination are depicted in Figure 24. The changes in cell structure under the influence of viral reproduction were observed for three days up to the formation ‘owl’s eye’, an indication of CMV infection, and the subsequent complete destruction.
The continuous development of new methods for the synthesis of non-toxic QDs and appearance of new applications in medicine and biology will undoubtedly contribute to successful solution of challenges of medicine of the future.
4.2. Luminescent nanothermometry
Temperature is a key physical quantity, which is of fundamental importance both in itself and as a parameter for measuring other physical properties. Among all sensors, temperature sensors have the largest share, accounting for 75 to 80% of the global market[724]. Monitoring of local temperature at a nanoscale is a relevant task of nanoscience and nanotechnology; solution of this problem is important for the development of micro- and nanoelectronics, integrated photonics and nanobiotechnology. Exact measurement of the local temperature with a high spatial resolution is still a very complicated task for usual thermometers due to the insufficient contact surface area between the thermometer and the object/area that is measured. Therefore, quantum dots are of considerable interest for optical nanothermometry owing to the small size and unique optical properties. Irrespective of the type of QD material, these properties depend on changes in the ambient temperature. Nanoparticles absorb light and then they convert the absorbed energy either into optical energy via emission or into thermal energy via various non-radiative mechanisms[725]. Quantum dots are characterized by high PL quantum yield, narrow luminescence band, flexible selection of the excitation wavelength, high stability to photodegradation compared to traditional organic fluorophores and a broad spectral range of operation due to the quantum size effect[726-732].
Wang et al.[733] reported a concept of using QDs as temperature sensors and studied PL of CdTe nanocrystals where the PL intensity \( I \) decreased linearly with temperature in the 303 – 333 K range (30 – 60 °C). The sensitivity \( S \) of this sensor was 1.1% K–1. The maximum of the luminescence spectrum occurred at \( \lambda_m \) of 518 nm upon excitation at 350 nm. On heating to higher temperatures, irreversible quenching took place, caused by oxidation and decomposition of the organic stabilizer. The use of QDs as colloidal solutions is not always convenient from the practical standpoint, because a film obtained by evaporation cannot be transferred to other surfaces and reused. To solve this problem, Liang et al.[734] prepared ultrathin films by layer-by-layer assembly of CdTe QDs and layered double hydroxide (LDH) and used them for temperature measurements in the range of 296 – 353 K (23 – 80 °C). It was shown that temperature rise is accompanied by a fivefold linear decrease in the luminescence \( I \) and a shift of \( \lambda_m \) from 558 to 568 nm. The \( S \) values for these characteristics were 1.47% K–1 and 0.193 nm K–1, respectively, and the structures showed a reversible change in these characteristics in eight successive heating – cooling cycles. Data on the temperature sensitivity of CdTe QDs and advantages of the composite structure are summarized in Table 1. In the case of a QD solution or a film, quenching is caused by only the temperature dependence of the non-radiative relaxation rate, whereas in the composite, there appears an additional quenching factor: reversible QD aggregation. Furthermore, inorganic LDH is more stable than the organic matrix. The synthesis of layered composite from QDs and polydiallyldimethylammonium (PDDA) chloride demonstrated that after 5 hours of UV irradiation, PL intensity decreased by 55.6%, while \( I \) of the CdTe – LDH luminescence decreased by 38.7%.
Apart from the absolute intensity and spectral shift, the ratio of \( I \) for different luminescence bands and the PL lifetime \( \tau_0 \) can serve as temperature-sensitive parameters. The use of these values to detect temperature in the range of 80 – 360 K was demonstrated by Kalytchuk et al.[736] in relation to colloidal CdTe QDs embedded into a sodium chloride protective matrix (CdTe@NaCl). The samples exhibited exciton and defect-related luminescence, and the intensity ratio of appropriate bands \( I_{x}/I_{d} \) formed the basis for ratiometric temperature measurement. This approach does not depend on the concentration or other local inhomogeneities of the probe and reduces the effect of factors that change the absolute intensities. The dependence of this parameter on \( T \) was non-linear and was described by a third-degree polynomial. In these cases, sensor is often characterized by pseudo-linear absolute and maximum relative \( S \) values, which were 0.007 K–1 and 0.61% K–1 for CdTe@NaCl at 199 K. The use of \( \tau_0 \) as the temperature-sensitive parameter also eliminates the effects of concentration or probe geometry as well as the light intensity scattering and fluctuations from the excitation source. Study of the lifetime of the defect-related PL of the composite demonstrated that this characteristic follows a non-linear dependence and can be effectively used for temperature measurement in the 80 – 320 K range. The pseudo-linear and relative \( S \) values at 320 K were 1.9 ns K–1 and 52.8% K–1, respectively. The obtained values markedly exceed the sensitivity of CdTe-based probes functioning by measuring the exciton luminescence lifetime[735]. The embedding of CdHgTe QDs into the sodium chloride matrix afforded a sensor operating in the near-IR range[178]. It was found that increase in the temperature of CdHgTe@NaCl from 80 to 340 K is accompanied by a linear shift of the luminescence maximum from 875 to 915 nm, characterized by absolute and relative S of 0.15 nm K–1 and 0.02% K–1, respectively. Simultaneously, the PL lifetime decreases from 77 to 55 ns and is described using a stretched exponential function. The absolute value of pseudo-linear S was 0.09 ns K–1, while the maximum relative S was 1.4% K–1 at T = 80 – 85 K (see Table 1). The CdTe@NaCl and CdHgTe@ NaCl composites demonstrate a high photothermal stability and can also be used as luminescence thermometers for non-invasive non-contact estimation of the local temperature in various modes: ratiometric, spectral and temporal ones.
The temperature determination based on PL quenching and the spectral shift of the luminescence band was demonstrated by Maestro et al[737]. As sensors, the authors used CdSe QDs excited in the single- (SPE) and two-photon (TPE) modes. The two-photon excitation makes it possible to localize the luminescence range, which provides a higher spatial resolution, and to minimize the influence of autofluorescence. In both excitation modes, a temperature rise in the range of 303 – 333 K (30 – 60 °C) induces a 5-nm red shift of the PL band, but the changes in intensity are considerably different. In the case of single-photon excitation, I decreases by 25%, while in the case of two-photon excitation, it decreases by 75%. This is due to the strong temperature dependence of the two-photon absorption cross-section. Maestro et al.[737] demonstrated the application of these nanocrystals for visualization of temperature gradients in biocompatible liquids and their potential for intracellular imaging.
A modern approach of luminescent temperature monitoring is the use of machine learning (ML). Lewis et al.[738] utilized this approach for measurements of T in microfluidic devices using the luminescence of CdTe QDs, which were embedded into the PR48 resin to form a sensitive channel. The authors noted that the accuracy of temperature determination for the study of biological processes in devices of this type is limited to approximately 1 K over a range of tens of degrees. This limitation was overcome by the developed machine learning algorithm, which was optimized for temperature measurement in two different ranges, 10 – 300 and 298 – 319 K. Data on the temperature dependence and lifetime of the PL band were applied to the input of the neural network. In the low-temperature region, the attained accuracy was 7.7 K, or 0.4 K in the case of training over the range of 100 K or more. For the high-temperature region, the accuracy was 0.1 K. The demonstrated use of ML technique for increasing the accuracy of temperature measurement in the microfluidic media opens up prospects for enhancement of biological studies and expansion of micro- and nanofluidic applications.
Albahrani et al.[739] proposed a procedure for the use of CdSe/CdS/ZnS quantum dots to measure the temperature and pressure in thin-film liquid flows. Solution of this problem is needed for characterization of elastohydrodynamic lubrication of various mechanical components, e.g., gears, bearings, cams, followers, etc. Quantum dots were mixed with squalane, which acted as a model lubricant with known rheological properties. The authors revealed a linear relationship between the PL energy and temperature in the 295 – 393 K range, characterized by S = 0.32 meV K–1. It was noted that the mentioned QDs also have prospects for application in micro- or nanofluidics, nanoectronics, photonics, biophysics and biomedicine.
The use of CdSe/ZnS QDs for the fabrication of a temperature-sensitive composite based on silicone (PlatSil® SiliGlass) using inkjet printing was demonstrated by Birchall et al[740]. Additive manufacturing technologies make it possible to print sensors on the surface of various materials and endow them with the desired geometric characteristics. The resulting composite demonstrated a linear decrease in the PL intensity in the range of 303 – 333 K (30 – 60 °C) and had S = 0.8% K–1. This was accompanied by a red shift of the luminescence maximum, which also followed a linear dependence and had an angular coefficient of 0.068 nm K–1. As benefits of the spectral method, the authors noted the independence on QD concentration and excitation power.
Tycko[742] used the CdSxSe1–x/ZnS quantum dots to design a temperature-sensitive paint for real-time temperature monitoring in the magic-angle spinning nmR spectroscopy (MAS nmR). Quantum dots of two different sizes, emitting at 540 and 620 nm, were mixed with the VGE-7031 varnish and applied on a surface to give a thin film. As the temperature was increased from 10 to 323 K, the photoluminescence maxima of the film underwent a 18 nm red shift. Meanwhile, at temperatures below 50 K, large errors appeared due to very small shifts of λm.
Ruiz et al.[184] proposed a nanothermometer using Ag/Ag2S nanocrystals as multi-parameter sensors functioning in the second biological window (1 – 1.3 mm). Quantum dots demonstrate a non-linear temperature sensitivity of luminescence intensity, which amounts to 3% K–1 at room temperature. Apart from the temperature-dependent quenching, the infrared emission of QDs undergoes considerable shift from 1235 to 1311 nm on heating in the 288 – 323 K (15 – 50 °C) range, which allows measuring the temperature irrespective of the QD concentration with the thermal sensitivity S = 2 nm K–1. The implementation of the ratiometric mode through monitoring of the intensity ratio at 1235 and 1311 nm wavelengths provides an almost temperature-independent sensitivity of 2% K–1.
The ZnS – AgInS2 nanocrystals can also be used as a temperature sensor[742]. A two-component luminescence sensor for simultaneous measurement of pressure and temperature was proposed by Kameya et al[747]. Owing to a broad spectrum of QD excitation, it is possible to avoid the overlap of spectral signals of various sensor components with the same excitation wavelength, which cannot be attained when a system with two dyes is used.
Marin et al.[743] performed temperature measurements using CuInS2 QDs passivated by 3-mercaptopropyltrimethoxysilane, which acted as a solvent, a source of sulfur and a stabilizer. The PL quantum yield for the obtained nanocrystals was approximately 6%, being increased to 55% after coating with ZnS shell. A polymer film with nanocrystals was manufactured and employed for detecting the temperature in the range from 140 to 340 K upon excitation at 405 nm. To determine the temperature, the PL spectral shift was analyzed, particularly, the spectrum was deconvoluted into three Gaussian components, then the ratio of the sum of integrated intensities of the long-wavelength bands to the intensity of the component with a maximum at 642 nm was calculated. The S value of the composite non-linearly increased with increasing T and was more than 1% K–1 at temperatures above 280 K. The proposed sensor is promising for the in vivo luminescence thermometry for biological applications owing to the absence of toxic metals in the material.
Zhang et al.[744] described a system for temperature measurement based on non-toxic CuInS2/ZnS QDs encapsulated into amphiphilic micelles suitable for intracellular and in vivo applications. Micelles of 10.1 ± 2.5 nm size exhibited intense PL with a luminescence band at approximately 650 nm and S = 2.0% K–1, which does not depend on the pH, ionic strength or the protein concentration. It was found that at a concentration of 300 mg mL–1, micelles have no cytotoxicity against HeLa or PC-3 cells. The indicated structures exhibit high intracellular sensitivity and a linear correlation between the PL intensity and temperature, which provide accurate monitoring and prospects for hyperthermia applications.
A trend in the development of QD-based nanothermometers is to use structures emitting simultaneously in two ranges. Thus, in a single QD, there are several excited states of various natures, each being responsible for a particular PL band with an individual temperature dependence. In this case, the intensity ratio is detected, instead of the absolute intensity. This allows self-calibration of the system, thus increasing the accuracy and reliability. Liu et al.[745] reported a nanothermometer with two luminescence bands in the visible and near-infrared ranges based on the core/barrier/shell quantum dots – PbS/CdS/CdSe in PMMA. The device provided accurate measurements and high spatial resolution at the micro- and nanoscale as a result of simultaneous measurement of a number of temperature-dependent parameters. The S value of the sensor, which was 1.22% K–1 in the 180 – 300 K temperature range, was provided by the ratiometric response based on integrated intensities of bands with maxima at 670 and 910 nm, corresponding to the luminescence of CdSe and PbS. In addition, a linear temperature dependence was also followed by the shift of PL maxima and by a change in the lifetime (see Table 1). The stability of characteristics was verified in five heating – cooling cycles. The many-parameter temperature determination enables self-calibration and increases the accuracy of nano-sized thermometers.
Zhao et al.[746] proposed the PbS/CdS system with two luminescence bands as the temperature sensor. One band was located at 480 nm and corresponded to luminescence of the CdS shell, while the other one had a maximum at 630 nm and was associated with the PbS core. For studying the temperature dependences, QDs were placed into a PMMA matrix and excited with light at 400 nm. In the low-temperature region (120 – 150 K), the intensity ratio of the bands virtually did not change, while in the 150 – 280 and 280 – 373 K ranges, linear dependences with coefficients of 0.113 and 0.015 K–1, respectively, were observed. The PbS luminescence band was blue-shifted with increasing temperature. In the 230 – 350 K range, the dependence was linear with S = 0.336 nm K–1. In addition, the PL lifetime increased from 400 to 3300 ns as the temperature decreased from 373 to 120 K. The sensitivity in the mode of \( \tau_0 \) measurement was 14.1 ns K–1 in the range of 150 – 350 K. The linear response in the ratiometric, spectral and temporal modes of operation makes PbS/CdS QDs promising sensors for local temperature measurement with a nanoscale spatial resolution.
4.3. Quantum technologies: photon sources and detectors and memristor structures
Quantum dots have become widespread as the basis for light-emitting diodes that have higher efficiency than organic compounds[748]. A distinctive feature of light-emitting diodes with a QD-based conversion layer is the possibility of controlling the luminescence spectrum owing to the specified QD size distribution and a broad absorption spectrum. QD-based light-emitting diodes are already used in household light sources, coming to replace conventional (semiconductor, organic, hybrid) LEDs. Thus, the fabrication technology of new generation QLED displays started to be widely used.
Quantum dots also formed the basis for high-performance, but still exceptionally compact laser media. It was a challenging task to attain generation in semiconductor nanocrystals, because several excitons should be excited to produce a population inversion in QDs. This was first done by V.I.Klimov’s research team in close-packed layers of CdSe nanocrystals of 1.2 nm size[170]. Subsequently, a method for laser generation in QDs without excitation of multi-excitons was proposed for structures with distributed Bragg gratings in quantum wells, dots and with quantum cascades (see Ref. [749] and references therein).
Owing to the photon antibunching inherent in single QDs, they may perfectly serve as the basis of single photon sources, a key element for quantum technologies. Most often, molecular epitaxy, which allows QDs to be precisely positioned on substrates or inside optical waveguides and microresonators, is used for this purpose. One more promising application of QDs in quantum technologies is implementation of quantum memory devices[749].
Quantum dots, which possess a broad absorption spectrum and a specified emission range, represent an ideal base for various detectors and light converters. For example, QDs can markedly extend the working spectral range of conventional detectors to near- (1.3 – 1.5 mm) and medium- (20 – 200 mm) IR ranges when they are used on a photoactive Si surface. The advancement of detector devices into the IR region meets today’s demands of optoelectronic technology and telecommunications, new challenges of quantum optics and non-invasive medical diagnosis. Furthermore, QDs can be easily integrated into various integrated photonic devices[749, 750].
Along with memristor layered nanostructures based on inorganic materials[751-754], hybrid organic/inorganic nanocomposites (HOINs) using colloidal semiconductor quantum dots in a polymer matrix are promising functional media for non-volatile resistive memory cells, or memristors[755, 756]. Currently, studies of HOIN-memristors are being actively developed owing to their relatively low cost, easy manufacture by spin coating[755-772], good cycling stability (> 103 cycles)[760, 767], the possibility of fabricating flexible electronic devices[768, 762-764] and memory chips with crossbar architecture[765, 770, 771].
In these devices, the information is stored as a charge localized on QDs during the charge carrier transport through the memristor active layer (Table 2)[755-772]. As a rule, QDs act as electron traps, providing controlled formation or destruction of conductive electrical channels between the electrodes in a polymer matrix [e.g., PMMA; polyvinylpyrrolidone (PVP); polyimide (PI), etc.] under the action of external control voltage U[757-765, 767-772]. The controlled formation or destruction of conductive channels of anionic vacancies, e.g., sulfur vacancies Vs (Ref. [757]), and metal ions, e.g., Ag+ (Refs [757, 765]), is also possible.
The application of voltage U > 0 induces the ‘Set’ procedure, and the memristor switches from the initial high resistance state (HRS) to the low resistance state (LRS), or from the switched-off to the switched-on state. The ratio of the HRS to LRS currents defines the memory window of a memristive cell, which is > 103 (see Table 2). Subsequently, when U < 0 is applied, the ‘Reset’ procedure is implemented, and the memristor switches from LRS to HRS. In HOIN-memristors, the bipolar switching mode is implemented[757-765, 767-772] even when |U| < 1 V (Refs [757, 765, 769, 771]) from the first ‘Set’ procedure. These low-voltage resistive memory cells require no electroforming, which is an additional engineering advantage over memristive devices that require preliminary electroforming[749, 750].
Charge localization on QDs leads, as a rule, to the space charge limited current (SCLC) in HRS and Ohmic type of current in LRS (see Table 2)[767, 768, 757-765, 770-772].
If conductive channels with cross-sections commensurable with the size of a single charge trap appear in the active layer, quantum conductors with conductivity \( G_0 = e^{2}/(\pi \hbar) \approx 77.5 mS \) are formed. This, in turn, gives rise to discrete resistive states in the memristor, with integer and/or semi-integer values of \( 0.5G_0 \), \( 1G_0 \), \( 1.5G_0 \), \( 3G_0 \), \( 4G_0 \) and \( 5G_0 \)[757], and the possibility of fabrication of multi-level non-volatile memory cells.
The change in the resistive state (LRS ↔ HRS) of an HOIN memristor based on QDs may be induced by light, which implies the existence of an additional external optical control channel[755, 756, 758, 765]. This control method improves the performance characteristics of the memristor, for example, this leads to a decrease in the switching voltage and the corresponding HRS current[765]. Furthermore, under external electrical and/or optical stimulation, HOIN memristors can emulate the operation of biological synapses and demonstrate high plasticity[758, 765], which opens up prospects for creating solid models of synapses for neurochips, elements of neurocomputing systems and artificial neural networks[755, 756].
The switching parameters and characteristics of memristors are determined by the material of electrodes, charge carrier traps and the polymer matrix. A typical HOIN memristor has a layered vertical sandwich structure consisting of two (top and bottom) electrodes and a functional (active) layer between them. The controlled resistive switching induced by an external electric field and/or optical stimulation takes place particularly in this layer[757-760, 762-765, 767-772]. Horizontal HOIN memristors in which two electrodes (the left- and right-hand ones) and the active layer between them are located in one plane on an isolating substrate were also reported[756, 761]. For example, Fu et al.[761] studied a multi-level memory cell with a photoinduced change in the phase composition based on MoS2 QDs and graphene electrodes located on the Si/SiO2 substrate.
5. Conclusion
The modern methods for QD synthesis in the solid matrix and in colloidal solutions considered in this review clearly demonstrate a quantum leap that has recently taken place in this area. The previously developed methods for QD synthesis in a solid matrix such as glass melt quenching followed by low-temperature annealing and the sol – gel method were supplemented by ion implantation, ion exchange and femtosecond laser irradiation. New methods allow more precise control of the QD shape and size, which makes the obtained QD ensembles more uniform and their properties more definite and predictable. Synthesis in non-aqueous and aqueous colloidal solutions gave new QDs in terms of both the chemical composition and molecular composition of the stabilizing shells. This development of synthesis methods resulted in enhancement of QD properties and expansion of the scope of their applicability.
Analysis of various processes for the synthesis and properties of QDs revealed causes for the influence of the synthesis method on the QD behaviour, namely generation of different atomic defects and different structures of the interfaces between QDs and their environment. Since different types of atomic defects and interface structures give rise to different electronic features of QDs, the exciton spectra and dynamics change, which can be used to study the proper QDs. In addition, owing to the relationship between the QD optical properties and crystallization and passivation techniques, it is possible to expand the areas of practical use of QDs.
The controlled synthesis of QDs with specified properties suggests that QDs will be used more extensively in the luminescent sensing of gases, heavy metals and toxic compounds. The luminescence labelling and imaging of tissues and cells in vivo and in vitro would become customary in biomedicine in a near future, and the quantum dots would become major components of the element base for photovoltaics, photodynamic therapy, quantum cryptography, laser technology, luminescent temperature sensors, luminescent pH indicators and optoelectronic devices. In addition, from general considerations, it can be assumed that photoactive QDs would become the base for photocatalysts and photosorbents operating under the exposiure to light over a wide range of wavelengths.
Among the currently unsolved issues in this field, mention should be made of providing the reproducibility of the atomic structure of quantum dots and the possibility of scaling up their manufacture. The active work along this line indicates that these challenges would be solved in the near future.
6. List of abbreviations and symbols
CCD — charge coupled device;
CMV — cytomegalovirus;
DA — donor – acceptor;
HOIN — hybrid organic/inorganic nanocomposites;
HRS — high resistance state;
IC — index of cytotoxicity;
ITO — indium tin oxide;
LA — longitudinal acoustic phonon;
LDH — layered double hydroxide;
LO — longitudinal optical phonon;
LRS — low resistance state;
MAS nmR — magic-angle spinning nmR spectroscopy;
MEG — multi-exciton generation;
ML — machine learning;
MTT — methyl thiazolyl tetrazolium;
OLED-QDs — organic light emitting diode – quantum dots;
PEDOT : PSS — poly(3,4-ethylenedioxythiophene) : poly-(styrene sulfonate);
PEN — polyethylene naphthalate;
PET — polyethylene terephthalate;
PF — Poole – Frenkel emission;
PI — polyimide;
PL — photoluminescence;
PMMA — poly(methyl methacrylate);
PMSSQ — polymethylsilsesquioxane;
PSF — point spread function;
PT — phase transition;
PVA — polyvinyl alcohol;
PVP — polyvinylpirrolidone;
QCSE — quantum-confined Stark effect;
QDs — quantum dots;
REE — rare earth elements;
RSF — regenerated silk fibroin;
RT — resonant tunnelling;
SCLC — space charge limited current;
SERS — surface enhanced Raman scattering;
SPE — single-photon excitation;
TBP — tri-n-butylphosphine;
TCD — tissue cytopathogenic doses;
TEE — thermoelectron emission;
TEM — transmission electron microscopy;
TERS — tip enhanced Raman scattering;
TGA — thioglycolic acid;
TO — transverse optical phonon;
TOP — tri-n-octylphosphine;
TOPO — tri-n-octylphosphine oxide;
TOPSe — tri-n-octylphosphine selenide;
TPE — two-photon excitation;
TTA — 4,4,4-trifluoro-1-(thiophen-2-yl)butane-1,3-dione;
X/Y — core/shell quantum dots: the core is made of X and the shell is made of Y;
X : Y — Y-doped X quantum dots;
X@Y — X quantum dots embedded in Y matrix;
\( T \) — absolute temperature;
\( T_g \) — glass transition temperature;
\( T_m \) — matrix melting temperature;
\( k \) — Boltzmann constant;
\( E_{n,l}^{e(h)} \) — energy states for electrons (holes);
\( n \) — principal quantum number;
\( l \) — orbital quantum number;
\( \hbar \) — Planck’s constant;
\( e \) — electron charge;
\( m_{e(h)}^* \) — effective mass of an electron (hole);
\( R \) — radius of a spherical nanocrystal;
\( E_{g}^{eff} \) — effective band gap for quantum dots;
\( E_g \) — bulk semiconductor band gap;
\( \mu \) — reduced effective mass;
\( k_{n,l} \) — wave vector;
\( \omega \) — frequency;
\( \varepsilon \) — dielectric constant;
\( E_{Ry}^* \) — exciton Rydberg energy;
\( H \) — half-width of the spectral absorption (or luminescence) band of a QD ensemble;
\( \Delta r \) — size distribution of nanocrystals in an ensemble;
\( d \) — QD diameter;
\( \lambda \) — position of the long-wavelength absorption maximum;
\( \hat{s} \) — electron Pauli matrix;
\( \hat{J} \) — hole Pauli matrix;
\( \alpha_0 \) — lattice constant;
\( \varepsilon_{exch} \) — exchange strength constant;
\( J \) — total angular momentum;
\( M \) — projection of the total angular momentum;
\( \Delta \) — hyperfine splitting;
\( \Delta_{\text{int}} \) — crystal field splitting;
\( \Delta_{\text{asym}} \) — splitting arising from QD ellipticity;
\( \gamma \) — degree of ellipticity;
\( c \) — semi-major axis of an ellipse;
\( b \) — semi-minor axis of an ellipse;
\( \Delta_{ss} \) — Stokes shift;
\( E_d \) — donor binding energy;
\( E_a \) — acceptor binding energy;
\( r_d - r_a \) — distance between the donor and the acceptor;
\( t \) — time;
\( \tau_{th} \) — relaxation time of thermalization;
\( \tau_{au} \)τau — relaxation time for the Auger process;
\( \tau_{re} \) — relaxation time for exciton recombination;
\( \tau_0 \) — luminescence lifetime;
\( m \) — average number of quencher molecules per donor;
\( \tau_D \) — luminescence lifetime of the donor without a quencher;
\( k_q \) — quenching rate constant;
\( \beta \) — band gap temperature coefficient;
\( A_F \) — Fan parameter;
\( \langle n_s\rangle \) — Bose – Einstein factor for phonons with the \( \hbar \omega \) energy;
\( \Theta \) — effective phonon temperature;
\( S_{hr} \) — Huang – Rhys parameter;
\( w \) — half-width of the optical band of a single nanocrystal;
\( \sigma \) — exciton – acoustic phonon coupling coefficient;
\( A_b \) — exciton – longitudinal optical phonon coupling coefficient;
\( \Delta_w \) — homogeneous broadening of the optical band of a single QD;
\( \Delta_I \) — inhomogeneous broadening of the optical band of a QD ensemble;
\( \Delta_T \) — temperature-dependent broadening of the optical band of a QD ensemble;
\( \eta \) — efficiency of radiative transitions;
\( E_q \) — activation energy for quenching;
\( I \) — photoluminescence intensity;
\( I_0 \) — photoluminescence intensity without quenching;
\(g^{(2)}(\tau) \) — second-order cross-correlation function;
\( \sigma_{X,Y} \) — variance of reconstructed transverse coordinates;
\( \sigma_{PSF} \) — width of the point spread function;
\( N \) — number of photons in the image;
\( \xi \) — CCD pixel size;
\( \varphi \) — background signal;
\( S \) — temperature sensitivity;
\( \lambda_m \) — photoluminescence maximum wavelength;
\( U \) — control voltage;
\( G_0 \) — conductance quantum.
Acknowledgements
The authors are grateful to the RF Ministry of Science and Higher Education for the support: project FUWF-2024-0010 (S.V.Rempel and Yu.V.Kuznetsova), project FEUZ-2023-0014 (I.A.Weinstein, A.S.Vokhmintsev and S.S.Savchenko); I.Yu. Eremchev and A.V.Naumov are grateful to the Moscow State Pedagogical University (theme of the state assignment for the RF Ministry of Education No. 124031100005-5). A.A.Rempel wishes to thank post-graduate students N.S.Belova-Kozhevnikova, A.S.Vorokh and I.D.Popov and Professor Dr. Andreas Magerl for the joint experimental work on quantum dots.
References


















































































































































































































































































































































































































































































































































































































































































































































![Comparison of the performance of QD-based luminescent nanothermometers. Refs. [178, 184, 733-746]](/storage/images/resized/Fij8wF4j98fTvtGss0lVqMfEBJLbfqCfn7w4MJF7_xl.webp)
![Characteristics of memristive structures based on colloidal QDs. Refs. [757-765, 767-772]](/storage/images/resized/QYZZx70Jc41gp4aiLJgMIS9EipIQv5NLf7kE0MLi_xl.webp)
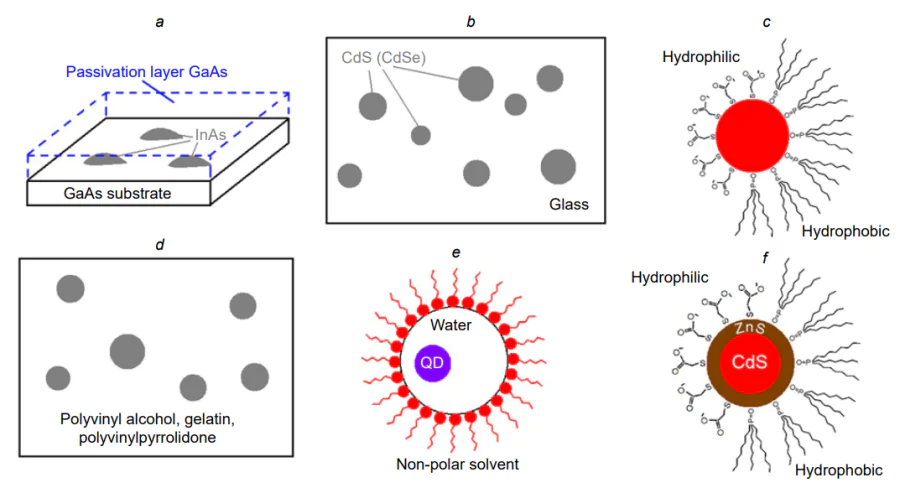
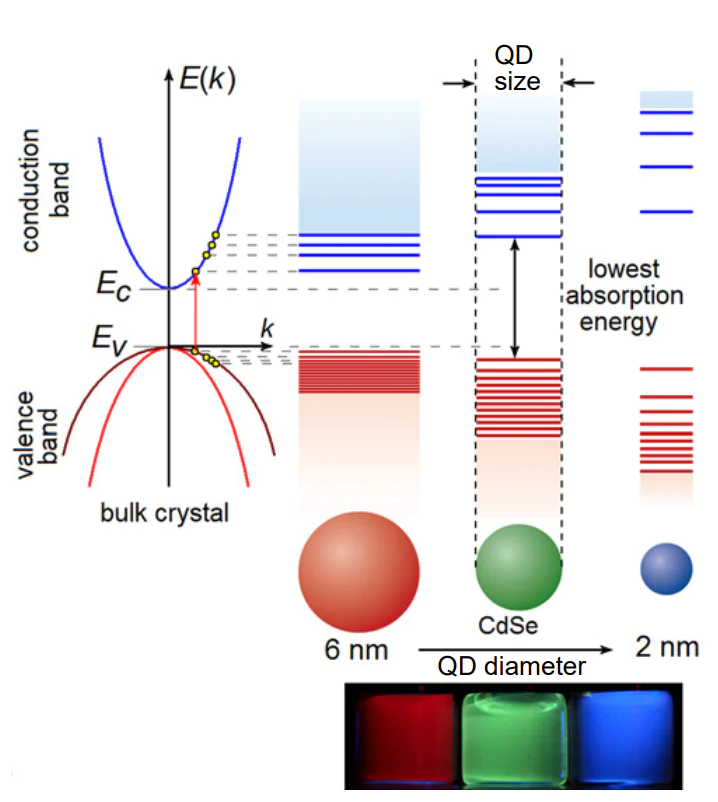
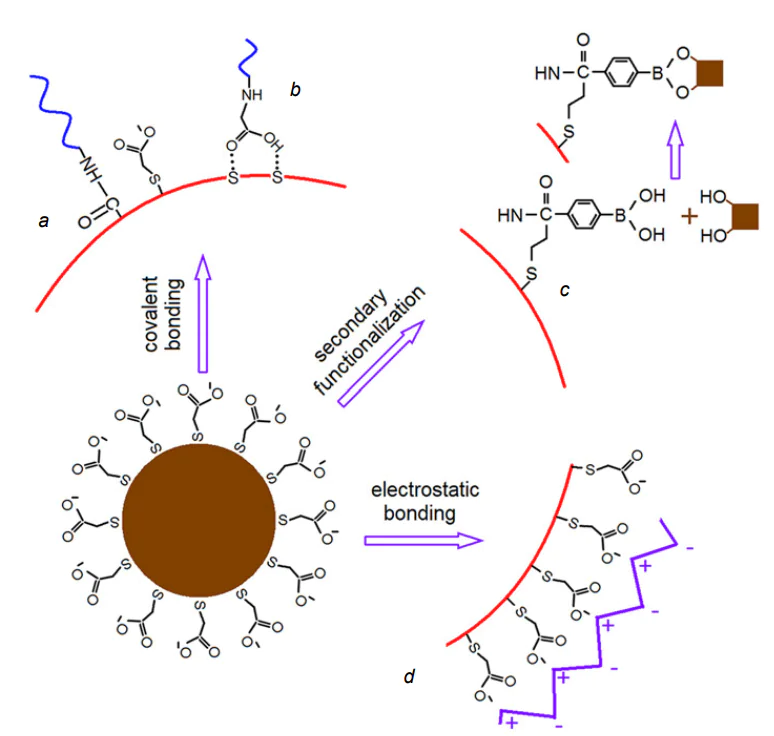
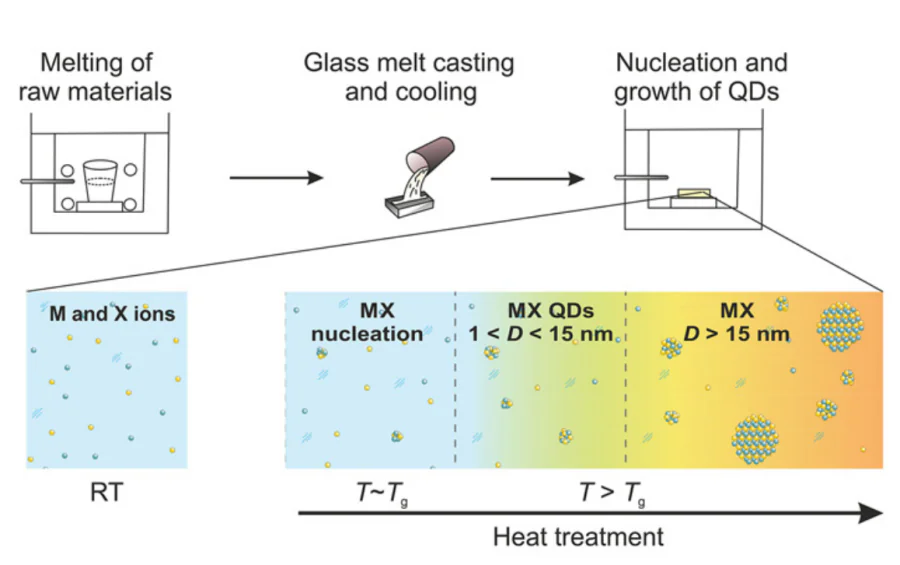
![Basic diagrams of QD synthesis in a solid matrix: (a) sol–gel method[266]; (b) ion implantation[269]; (c) ion exchange[270]; (d) femtosecond laser irradiation.](/storage/images/resized/JoKeMEDjKOEDX2fMBm8Fpqk7cwVu6k1ekBLr49Tl_xl.webp)
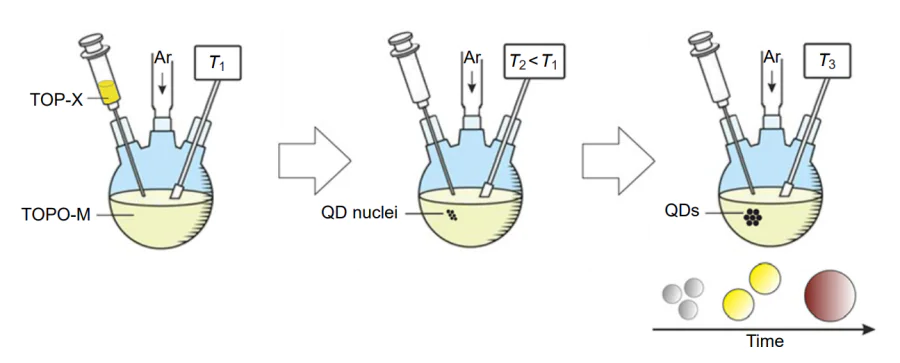
![Optical absorption spectra of CdSe (a) and CdS QDs (b) and their interpretation. In relation to the CdSe QDs (a), the disappearance of the exciton peak with increasing QD size dispersion is shown schematically (the sequence is from the bottom up)[72, 338].](/storage/images/resized/YcgqAsu9hNBbZdlBX3xJoAKRIiRuxysGoIyVEPJW_xl.webp)
![Effect of inhomogeneous broadening on the shape and structure of the optical absorption spectra of Ag2S QDs passivated with thioglycolic acid (TGA). The QD size distributions in ensembles, derived from analysis of TEM images, corresponding to the given spectra are shown on the right[375].](/storage/images/resized/3M9Jbb5JSSsDbgOwGE9n54NiJAXjyaPHA3c9ZufI_xl.webp)
![Size dependences of the energy of the QD ground exciton absorption transition obtained experimentally and using various semiempirical models for CdS QDs[52, 103, 329, 334, 379, 340-348], Ag2S QDs[126, 132, 141, 145, 150, 350-356], CdSe QDs[51, 78, 357-360] and PbS QDs[361-367]. Designations: 1[334], 2[340], 3[341], 4[342], 5[343], 6[344], 7[345], 8[346], 9[103], 10[347], 11[348], 12[52], 13[329], 14[349], 15[350], 16[351], 17[132], 18[150], 19[352], 20[145], 21[126], 22[353], 23[141], 24[354], 25[355], 26[356], 27[78], 28[357], 29[358], 30[359], 31[360], 32[51], 33[361], 34[362], 35[363], 36[364], 37[365], 38[366], 39[367].](/storage/images/resized/AAk9vM8csWryDzfA39nhk4UyvqP3I48Cps2FHoE4_xl.webp)
![Dependence of the Stokes shift energy on the confinement energy for PbS QDs (according to published data [366, 503, 504, 509-511]). Designations: 1[511], 2[366], 3[509], 4[503], 5 (see [510]) and 6[504].](/storage/images/resized/hHmnARcRnO8oLwEM81fW7M9mBiFIQZnzTykRS2UV_xl.webp)
![Key diagrams of recombination luminescence representing the size effect in the corresponding transitions ranging from a bulk crystal to small QDs The Figure was created by the authors using published data[100, 105, 107].](/storage/images/resized/VajsZ7veOaM6gtxc4G2xdIBHvV8Qkwol9gsTGBpw_xl.webp)
![(a) Absorption spectra of InP/ZnS QDs at various temperatures. (b) Analysis of the temperature behaviour of the exciton absorption band for InP/ZnS QDs of various sizes. The continuous lines show the approximation of the temperature-dependent shift by expression (23); dashed lines show the temperature dependence of the coefficient β[377, 620].](/storage/images/resized/bA0zWFBvoSwASuitgMBKBT0wqma99g9rbwm0PFj9_xl.webp)
![Simulated exciton absorption band for the InP/ZnS ensemble in comparison with experimental data. The inset shows the temperature-induced variation of absorption peaks for a single model nanocrystal[600]. (Published under the Open Access CC BY license).](/storage/images/resized/teQwLHS7WqO0pZOMxHwn01uPmwmdUoJ1AOUlgKEz_xl.webp)
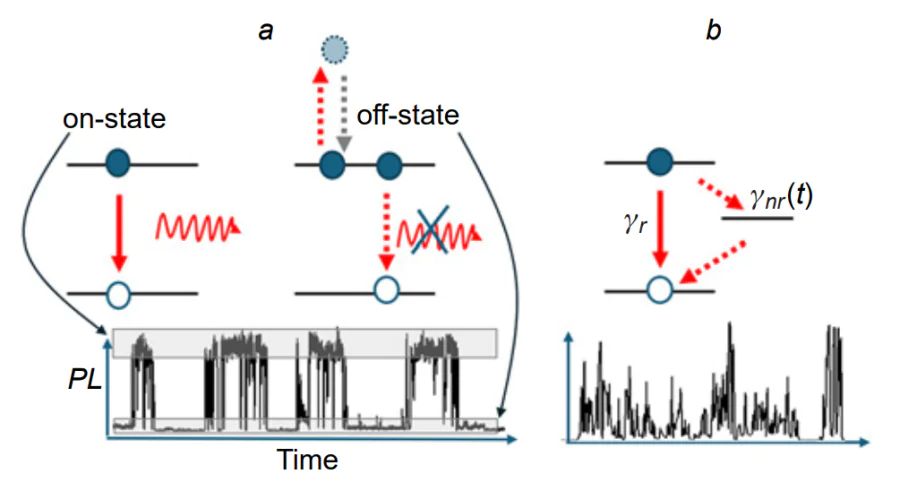
![Example of spectral diffusion of a single tetrakis(tert-butyl)terrylene molecule in polyisobutylene (a) and toluene (b) at cryogenic temperature (7 K)[669].](/storage/images/resized/98puwPnn0DmaptVB69mjtOHUXjWBsbhxxhVQ8xJB_xl.webp)
![Spectral dynamics of single quantum dots exemplified by colloidal CdSeS/ZnS QDs: (a) spectral trace of a single QD showing the presence of spectral diffusion, obtained by repeated measurements of the photoluminescence spectrum; (b) correlation between the position of the luminescence peak of a single QD and linewidth. The results were obtained similarly to the measurements repoered by Podshivaylov et al[638].](/storage/images/resized/HiAv3CU8klhw2bgk5KyEL4VNt5fzF5xRlYFLF6Lx_xl.webp)
![Raman spectra of quantum dots at room temperature: (a) thin-layer ensemble of CdSe/CdS/ZnS quantum dots on the surface of a glass substrate measured in the anti-Stokes mode[675]; (b) single CdSe quantum dot on a silicon substrate measured in the hyper-enhancement mode with the sample being placed in the gap between the tip of a probe microscope and a plasmonic nanoparticle as part of an enhancing nanostructured metasurface (combined SERS-TERS mode; surface- and tip-enhanced Raman scattering). The inset shows a map of the TERS signal intensity distribution in the sample plane; the locations for which the corresponding TERS spectra were measured are marked with numbers from 1 to 6[676].](/storage/images/resized/BCNOtiILF74AHaz1ebZ9M3d66xKs8LOtfMAwNr62_xl.webp)
![Sequentially recorded fluorescence images of single semiconductor colloidal CdSeS/ZnS QDs in the field of view of a wide-field epiluminescence microscope 20×20 μm2[677]. The acquisition time for one image is 100 ms.](/storage/images/resized/JW5ULwhXtt3zRcfVV7myndwRZdSOqt7ItIVWZdTp_xl.webp)
![Localization nanoscopy with quantum dots. (a) Schematic representation of the quantum dot images processing for reconstruction of the coordinates of the luminescence centres. Example of a luminescent image of a single quantum dot. (b) Distribution of reconstructed coordinates for a fixed spatial position of single CdSe/ZnS QD. (c) Dependence of the accuracy of reconstruction of the X and Y coordinates of single QD on the number of photocounts[667]. (d) Example of optical nanotracking of a CdSe/ZnS quantum dot.](/storage/images/resized/tvWIchKZMk8sbaOA3Rv2jCjU8yTku1FB7WhHq1UO_xl.webp)
![Index of cytotoxicity for aqueous colloidal solutions of CdS in various concentrations (green columns) after the synthesis and for precursors according to methyl thiazolyl tetrazolium (МТТ) assay data, CPT is camptothecin (control)[716].](/storage/images/resized/CEWHFcxiHeDYVHtgnRlSzBVh3XI2pfPBI4oTDCPH_xl.webp)
![Possible mechanisms of cellular uptake of nanoparticles and quantum dots depending on the shape, size, charge and molecules attached to the surface. Phagocytosis (1) and macropinocytosis (2) for aggregates and large nanoparticles; different mechanisms of pinocytosis (2–9) depending on the shape and attached molecules; direct uptake (10) and pore formation (11) for nanoparticles either positively charged and/or less than 10 nm in size[717]. The picture is published according to the Creative Commons Attribution 3.0 Unported License.](/storage/images/resized/tWP5L7npgCsS1AqlMtpbzTWlNazTiMzZsBcAnWMm_xl.webp)