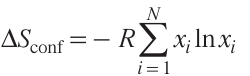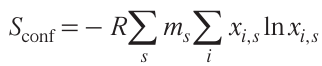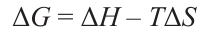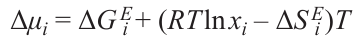Keywords
Abstract
The importance of high-entropy materials is dictated by the requirements of high-temperature technologies related to the problems of aviation and aerospace engineering, nuclear power engineering, metallurgy, and microelectronics. The significant interest in the materials mentioned is explained by a combination of unique physical and chemical properties such as high mechanical strength and hardness and chemical and thermal stability. This review gives analysis of studies that address the physicochemical properties of high-entropy oxides, carbides, and oxycarbides at high temperatures and illustrates the potential use of these results for the synthesis and operation of a broad range of materials under high-temperature treatment. It is shown that the search for optimal solutions for the development of refractory materials based on multicomponent oxides, carbides, and oxycarbides requires the use of integrated physicochemical approach, involving information on the thermodynamic properties, phase equilibria, and vaporization processes.
The bibliography includes 247 references.
1. Introduction
In recent years, considerable attention has been paid to the development and investigation of conceptually new materials with controlled physicochemical and mechanical properties. In the early 21st century, the interest has been focused on high-entropy materials (HEMs), mainly metal alloys and nitride coatings.
Multicomponent alloys consisting of five and more metals present in nearly equimolar amounts were proposed for the first time as high-entropy systems (high-entropy alloys, HEAs).[1-6] In particular, in 2022, according to the Web of Science data, 2845 papers devoted to HEAs were published.[7]
The review of Pogrebnjak et al.[1] analyzes and integrates the results of investigation of HEAs; establishes the regularities of structure formation and conditions of phase formation of the alloys; considers the thermodynamic relationships between the mixing entropy, formation of a single-phase solid solution, and the changes in the Gibbs free energy needed to maintain the solid solution stability; describes the potential of the computer simulation of HEA structure and properties; and illustrates the features of synthesis of nitride coatings based on multicomponent alloys.
The review by Rempel and co-workers [2] considers ways of the HEA synthesis and methods and results of computer simulation of high-entropy alloy structure and applications as corrosion-, heat-, and radiation-resistant materials. The attention is concentrated on the use of HEAs as protective coatings. In particular, recently Rempel and co-workers [3] illustrated the possibility of preparing high-entropy alloys based on AlTiZrVNb system from the corresponding oxides by aluminothermic co-reduction of the metals.
Although study of HEAs started less than 20 years ago, these alloys have already formed the basis for materials widely used in various fields of science and technology, including rocket and space, aircraft, and machine building industries, nuclear power engineering, and other.[8-10]
In comparison with HEAs, which include alloys and nitride compounds, studies of high-entropy oxides (HEOs) started only recently. The possibility of obtaining entropy-stabilized systems based on oxides was first shown in 2015.[11] The active studies of high-entropy oxides started immediately, which resulted in the appearance of several hundred publications in this area, which are surveyed in a number of reviews.[12-16]
Subsequently, the concept of high-entropy materials was extended to other classes of chemical compounds, including carbides [12, 17] (HECs) and oxycarbides [18] (HECOs), characterized by high thermal and chemical stability necessary for the design of ultra-high-temperature ceramics, in particular new-generation high-temperature protective coatings.[17]
A high-entropy system consists of quite a number of components, most often, in equal concentrations.[12-16] On the one hand, an increase in the number of components in the system is accompanied by the entropy stabilization of the chemical and phase composition, resulting in the formation of chemically homogeneous single-phase materials. Note that the high entropy of mixing corresponding to this system can be sufficient to counterbalance the positive contribution of the enthalpy of mixing to the total Gibbs energy of solution formation, especially at high temperatures.[4] On the other hand, the increase in the number of system components provides a variety of opportunities to change the composition of materials and, hence, to obtain a specified set of functional properties needed to solve a particular scientific problem.[12, 19] It should be specially emphasized that HEMs are promising for a very broad range of practical applications owing to the unique set of physicochemical properties [12-16] such as
— high mechanical characteristics, including mechanical strength, hardness, and fracture toughness;[14]
— chemical and thermal stability, which is important for the development of thermoelectric materials and ionic conductors;[7, 16]
— variety of electric properties ranging from insulators to conductors and semiconductors; samples possessing thermoelectric and ferroelectric properties were also obtained;[13]
— promising magnetic characteristics for the development of ferromagnetic and antiferromagnetic materials and magnetic insulators.[20]
Owing to the unique combination and the possibility of flexible optimization of physicochemical properties, high-entropy systems have been recognized as a basis for the design of a wide range of new materials useful in various fields of modern technology. Among the promising applications of HEMs, there are high-temperature technologies such as aviation and aerospace engineering and sustainable energy production, particularly, green energy storage and conversion.[19] The following HEMs are being developed now to pursue this goal:
— ultra-high-temperature ceramics, including new-generation high-temperature protective coatings,[17, 21, 22] particularly thermal barrier and environmental barrier coatings,[21, 22] used, among other purposes, for heat-protection systems of hypersonic aircrafts;[23]
— oxygen storage materials [24] and materials for oxygen separation from gas mixtures [25] and oxygen transfer in chemical looping processes,[24, 26] for example, for the separation of carbon dioxide after fuel combustion,[25] for hydrogen production by methane reforming (oxidation),[27, 28] and for synthesis gas production by methane oxidation;[28]
— anode materials for lithium-ion batteries;[29, 30]
— cathode materials for sodium-ion batteries;[31]
— electrode materials for supercapacitors;[32]
— materials for solid electrolytes of solid oxide fuel cells;[13]
— dielectrics for high-energy-density capacitors;[33]
— metal oxides such as TiO2 and ZnO in which a change in the band gap by adding other oxides is promising to increase the efficiency of dye-sensitized solar cells and perovskite solar cells;[13]
—catalysts for reactions of oxygen evolution;[34]
— catalysts for photocatalytic water splitting to produce hydrogen;[35]
— substrates for noble metals in carbon monoxide oxidation;[36, 37]
— noble metal supports for carbon dioxide reduction reactions.[38]
A unique combination of physicochemical properties, including superior refractoriness, was noted for complex HECs and HECOs in the (Hf0.25Zr0.25Nb0.25Ti0.25)C and (Hf0.25Zr0.25Nb0.25Ti0.25)(C0.5O0.5) systems, which were also characterized by high initial oxidation temperature and low rate of high-temperature oxidation.[18]
The oxidation and corrosion resistance of multicomponent carbides and oxycarbides [39-43] is fairly useful for the design of materials for critical applications, which should retain the service properties under extreme environmental impacts. It was found [18, 42, 43] that oxycarbide phases are more chemically inert to high-temperature oxidation with oxygen than the corresponding carbides, which allows HECOs to be recommended as the most promising superior refractory material candidates.
However, according to reviews,[12, 14, 15] the information on high-temperature thermodynamic characteristics is virtually missing even for the most studied high-entropy oxide systems. Analysis of the available literature on the high-temperature behaviour of multicomponent systems also indicates that the data on vaporization of high-entropy oxides and carbides are quite limited.[12, 17] The lack of information on the vaporization, phase equilibria, and thermodynamic properties of the considered systems at high temperatures markedly complicates the stable operation of materials under temperature extremes.
Hence, the relevance of synthesis and investigation of HEMs is dictated by the following key challenges brought about by the need to extend the use of these materials in modern materials science, especially at high temperatures:
1. Gaining information on the thermodynamic properties, which is critical for correct analysis of the possibilities of synthesis and application of HEMs. It is also noteworthy that a serious obstacle to high-temperature application of high-entropy oxides, carbides, and oxycarbides is phase instability of the materials after repeated high-temperature operation cycles, which may be caused, for example, by phase transitions in the condensed phase and selective vaporization of the most volatile components.
2. Development of new ultra-high-temperature materials, including modern heat protective coatings for parts of gas turbine engines of aircrafts and spacecraft, which should outperform the zirconium oxide ceramics, traditionally used to protect working surfaces from high-temperature oxidation.
3. Determination of the optimal compositions of HEMs and their thermal stability ranges in various media, which is important for development of new ultra-high-temperature materials required in the transport equipment, space systems, and manufacture and modernization of new-generation turbine power plants.
4. Identification of safe conditions for high-temperature processes involving materials based on high-entropy oxides, carbides, and oxycarbides.
Thus, analysis of the state-of-the-art studies on the design of HEMs for high-temperature technologies necessitates the development of an integrated physicochemical approach for predicting and implementing the potential of HEMs.
This review shows that for gaining information on the thermodynamic characteristics of complex high-entropy systems, it is reasonable to use combinations of various experimental methods and theoretical approaches including the following:
— high-temperature mass spectrometry, which provides unique data on the thermodynamic properties and vaporization processes of the studied systems up to 3000 K;
— modification of known empirical and semiempirical methods of calculation and prediction of thermal stability and liquidus temperatures of complex high-entropy systems;
— statistical thermodynamic models, for example, the model based on the generalized lattice theory of associated solutions, and a wide range of theoretical approaches for calculation and prediction of thermodynamic properties and phase equilibria of high-entropy systems.
The formation of a unified approach to predicting thermodynamic properties, phase equilibria, and vaporization processes of high-entropy oxides, carbides, and oxycarbides at temperatures of up to 3000 K is an important stage in the development of energy-saving systems, energy transportation, distribution, and use, and design of new-generation high-temperature protective coatings according to the priority areas in the development of science, technology, and engineering in the Russian Federation.
The use of above modern methods and approaches in the implementation of this review revealed the most important thermodynamic aspects of the high-temperature stability of various classes of high-entropy systems based on oxides, carbides, and oxycarbides. Thus, the present review not only arranges the currently available data on high-entropy compounds, but also reveals the most relevant high-temperature technologies in which these materials are in most demand.
2. High-entropy oxide systems
In 2015 and 2017, Rost et al.[11, 44] reported the first high-entropy oxide Mg0.2Ni0.2Co0.2Cu0.2Zn0.2O with the rock-salt structure (Fig. 1).
Similarly to HEAs, the high-entropy oxide Mg0.2Ni0.2Co0.2Cu0.2Zn0.2O is a multicomponent single-phase material. The cation sites in the structure are compositionally disordered like those in HEAs. However, unlike HEAs, Mg0.2Ni0.2Co0.2Cu0.2Zn0.2O has an ordered anion sublattice. Later, HEOs with different types of structure, including perovskites, fluorites, spinels, etc., were successfully synthesized. High-entropy oxides are complex oxide systems consisting of five or more metal cations in equimolar amounts and having a single-phase crystal structure.[7, 16] Both transition metals and rare earth elements (REEs) can be present in HEOs.[45-47] In the simple crystal structures of oxides, the ions are uniformly distributed in the crystal; therefore, these systems are characterized by high entropies of mixing.
The configurational disorder in HEOs characterized by high entropy of mixing is due to the fact that atoms of several elements may occupy the same lattice point, with the number of possible combinations being enormous.
A major factor responsible for stabilization of HEOs (Fig. 2) [7] is the configurational entropy, or the entropy of mixing, which should be greater than 1.5 R, where R is the universal gas constant. Cormack and Navrotsky [48] demonstrated that the configurational entropy of HEOs should exceed 1.609 R per mole of cations. According to published data,[7, 48] understanding of the role of configurational disorder in existing HEOs is currently an important step in the way towards rational design of materials with specified properties.
It was shown [11, 44] that the use of at least five metal cations in oxide systems usually results in the formation of a single-phase solid solution owing to the entropy stabilization effect. It was noted [11, 13] that increase in the configurational disorder and, hence, the entropy of the system is attained by introducing various metal cations into the cation sublattice, whereas the anion sublattice is filled only with oxygen ions and makes no contribution to the system entropy. However, according to McCormack and Navrotsky,[48] it is necessary to indicate the units of measure, since this statement refers to entropy per mole of cations. If the configurational entropy is calculated per mole of atoms, the anion sublattice contributes to this value.
It was noted [49, 50] that high entropy of mixing ensures thermal stability of systems, with the mechanical, physical, and chemical properties being retained. The ability to form a single-phase solid product is due to the emergent properties of the system, i.e., the properties that are absent in the separate system components.[7, 51, 52] Sarkar et al.[53-55] analyzed the effect of the entropy and enthalpy factors and the influence of definite electronic states on the physicochemical characteristics of high-entropy systems. The significance of the simultaneous influence of high entropy and a negative enthalpy, resulting in strengthening of the inter-ion bond, on the formation of stable single-phase structures was confirmed by Zhang and co-workers.[56] Analysis of the set of effects related to the influence of electronic configuration of ions on the HEO structure symmetry was reported by Rák et al.[57]
Four key factors characterizing HEMs have been proposed [11, 16] (Fig. 3):
(1) thermodynamic: high entropy of mixing, providing systems with thermal stability;
(2) structural: the crystal structure consists of atoms of different sizes, which randomly occupy the lattice sites, giving rise to lattice distortion;
(3) kinetic: cations of different elements have different diffusion kinetics, which prevents phase transitions and maintains stability of the system;
(4) cocktail effect: properties of HEMs are not equal to the sum of the properties of components and are unpredictable.
In the studies of high-entropy oxides, the efforts of researchers have largely been concentrated on rock-salt,[11, 44] perovskite,[24, 28, 30, 37, 47, 58-60] fluorite,[46, 61, 62] and spinel [34, 63, 64] structures.
It is known [47, 60, 65] that high-entropy perovskites (HEPOs) have a broad range of functional characteristics significant for practical application. The multicomponent perovskite oxides are among the most promising high-entropy oxides for the use in thermal protection, oxygen storage and transfer and as anode materials of lithium-ion batteries.[30, 66, 67] In addition, it was shown that HEPOs have a number of remarkable characteristics such as the unique capacity for oxygen transport and storage,[26, 28] and also catalytic,[68] photochemical,[13] electrochemical,[30, 59] thermoelectric,[69, 70] semiconductor,[71] magnetic,[72] and some other properties.
The HEPO-based materials are of interest for oxygen extraction from gas mixtures and oxygen transfer in chemical looping processes. A series of perovskites BaLnM2O5 + d (Ln = Y, La and M = Fe, Co) was obtained and investigated for the ability to take up and release oxygen.[26] All of the tested samples demonstrated fast and reversible uptake and release of oxygen on adsorption/desorption cycles with nitrogen and air (Table 1).
In addition, perovskites Ln0.5A0.5Co0.5Fe0.5O3 – δ (A = Sr, Ba) and La0.6Sr0.4Co0.8Fe0.2O3 – δ were studied as oxygen storage and carrier materials.[24] The indicated complex oxides have high oxygen storage capacity and undergo fast redox reactions; their major drawbacks include instability at high temperatures and in a reducing atmosphere, especially upon a significant number of operation cycles.[24]
Unfortunately, there are only scattered data on the physicochemical characteristics of HEPOs and virtually no systematic studies of either the effect of temperature on the stability of perovskites or the effect of the replacement of elements (e.g., within the same group) on the oxide characteristics.
In particular, the effect of alkaline earth metals on the properties of perovskites is addressed only in few works. It was established that the perovskite Ba0.4Sr0.4Bi0.2(Zr0.3Hf0.3Ti0.2Fe0.2)O3 can be used as a support for ruthenium catalysts, which increases the catalyst activity in the carbon monoxide oxidation at elevated temperatures.[37] Materials based on La1 – xSrxAyFe1 – yO3 (A = Ni, Co, Cr, Cu) were tested in the production of syngas by oxidation of methane [28] at 1273 K. The La0.7Sr0.3Cr0.1Fe0.9O3 sample remained stable for at least seven cycles of methane oxidation – reduction. All tested materials are suitable as oxygen carrier materials in the chemical looping reforming.
Electrochemical and photochemical properties of high-entropy perovskite oxides attract special attention. In particular, they can be used in the perovskite solar cells owing to the possibility of varying the band gap of TiO2 or ZnO by introducing a large number of other oxides.[13] La1 – xSrx(FeNiMnCoCr)O3 – δ was considered as an air cathode for solid oxide fuel cells,[59] while [Bi0.1Na0.1La0.1Li0.1Ce0.1K0.1Ca0.2Sr0.2]TiO3 was tested as an anode material for lithium-ion batteries.[30]
A study of the structural, electronic, and magnetic properties of multicomponent perovskites based on cobalt and REE oxides (Gd0.2Nd0.2La0.2Sm0.2Y0.2)CoO3 demonstrated [71] that this system behaves as a multifunctional metal oxide semiconductor. Witte et al.[72] reported the synthesis and study of magnetic properties of multicomponent perovskites A(Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)O3 (A = Gd, La, Nd, Sm, Y). According to the authors, the magnetic properties of these perovskites can be caused only by the presence of competing magnetic exchange interactions within the cation sublattice.
It is known that the perovskite crystal lattice can undergo various kinds of distortions upon a change in the synthesis temperature or upon doping. Therefore, it is of interest to study promising barium titanate-based ceramics in which some barium atoms have been replaced by calcium atoms, and zirconium and transition metal (manganese, iron, cobalt) atoms have been introduced into the titanium sublattice: Ba0.9Ca0.1Zr0.05M0.10Ti0.85O3 (where M = Mn, Fe, Co).[73] In this study, particular attention was paid to conditions of synthesis, phase formation, and magnetic and optical properties of samples with the indicated composition. Magnetic susceptibility measurements showed the presence of magnetically coupled aggregates composed of different-valence atoms of a paramagnetic element with competing ferromagnetic and antiferromagnetic exchange interactions in the samples. The experimentally determined magnetic moments are important characteristics for the development of ferromagnetic and antiferromagnetic materials and magnetic insulators (Fig. 4).
Study of the optical properties of selected samples showed that the band gap virtually does not change upon replacement of transition metal atoms (manganese, iron, cobalt) in the perovskite structure.
Thermal barrier coatings (TBCs) are a major high-temperature application of HEOs. Yttria-stabilized zirconia (YSZ), the operation time of which is approximately 200 h at 1473 K and only 30 h at 1573 K, is still widely used as TBC.[74]
The search for TBCs that have a lower thermal conductivity and would be able to operate at higher temperatures and for longer times than YSZ is currently underway. The key for applicability of oxides as TBCs is a low thermal conductivity (below 1 W m–1 K–1) and stability at high temperatures.
Zywczak and co-workers [71] pointed out that most perovskite materials are stable at high temperatures. Among perovskites, mention should be made of zirconates applicable for deposition of thermal barrier coatings. The zirconates considered as TBCs include BaZrO3 with melting point of 2873 K, but relatively poor thermal and chemical stability; SrZrO3, which has better performance during cycling at 1523 K; and CaZrO3 with a lower melting point compared to that of YSZ and with a somewhat lower thermal conductivity equal to 2.0 W m–1 K–1.
The thermal conductivity of fluorite and pyrochlore oxides is lower than that of YSZ and they can be potential new materials for TBCs.[75-80]
The high-entropy pyrochlore oxides (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)2Zr2O7 and (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)2Hf2O7 are stable on heating to 1773 – 1873 K; they have low thermal conductivity and can be used to develop thermal barrier coatings.[76, 77] High-entropy oxides with a disordered fluorite structure (HEFOs) were reported [78-80] to have ultralow thermal conductivity, excellent phase stability, and radiation resistance; therefore, they can be used as thermal barrier coatings and radiation resistant materials. Cong et al.[78] demonstrated that the HEO (Y0.2Gd0.2Dy0.2Er0.2Yb0.2)2Hf2O7 (Fig. 5a) has a disordered fluorite structure with highly uniform distribution of REE cations and demonstrates phase stability at temperatures of up to 1973 K and compatibility with Al2O3 even at 1573 K.
Gild et al.[80] synthesized eleven fluorite samples. It is noteworthy that the obtained single-phase HEFOs have lower thermal conductivity than YSZ (Fig. 5b).
Pyrochlore HEMs can potentially be used as TBCs.[81] The authors [81] studied six samples of pyrochlore oxides obtained by solid-phase synthesis using six REE oxides (La2O3 , Nd2O3 , Sm2O3 , Eu2O3 , Gd2O3, and Y2O3) and ZrO2 . The high-entropy pyrochlores (5 RE1/5)2Zr2O7 were formed after heating to 1273 K and showed high sintering resistance and excellent thermal stability. The data on the temperature dependence of the thermal conductivities of pyrochlores (5RE1/5)2Zr2O7 presented in Fig. 6 indicate that the thermal conductivity of oxides was less than 1.0 W m–1 K–1 in the temperature range of 573 – 1473 K.
In the opinion of Li et al.,[81] high-entropy pyrochlores can be considered as solid solutions in which five REE cations in equimolar amounts occupy the same crystallographic positions in the pyrochlore structure in a random fashion. The difference between the cation masses and radii leads to large lattice distortions and strong phonon scattering in the materials. The lattice distortion, one of the four main effects in HEMs, may be a major factor responsible for the reduced thermal conductivity of these single-phase high-entropy pyrochlores.
The search for low thermal conductivity materials for thermal barrier coatings is being intensively carried out, particular causes for the reduced thermal conductivity of single-phase HEOs are being investigated, but rapid progress is likely to be achieved only with systematic experimental research and the use of models to calculate the thermal conductivity.[75]
Due to the constantly growing demand for energy and the concerns about global warming, considerable attention is given to advanced renewable energy technologies such as portable electronics, electric vehicles, and energy storage. To meet the growing demand for modern rechargeable lithium-ion batteries, a lot of effort has been devoted to studies of electrode materials with longer service life, higher lithium storage capacity, and improved cycle stability. It was shown [63, 64, 82] that high-entropy spinels have a uniform structure and can be used as anodes in lithium-ion batteries. Chen et al.[63] reported the synthesis of a new spinel type material (Mg0.2Ti0.2Zn0.2Cu0.2Fe0.2)3O4, which exhibited excellent lithium storage properties and provided a greater reversible capacity after 300 battery operation cycles.
The study of enhancement of the exchange bias in the Pt/Py/(Mg0.25(1 – x)CoxNi0.25(1 – x)Cu0.25(1 – x)Zn0.25(1 – x))O/MgO ferromagnetic/antiferromagnetic heterostructures performed by Meisenheimer et al.[83] showed a strong correlation of the electronic structure with magnetic and electronic properties. Specific characteristics of the permittivity [84] and superionic conductivity [85] were noted for oxide-based materials with the formula (MgCoNiCuZn)1 – x – yGayAxO (where A = Li, Na, K); therefore, they can be used in electrical engineering for lithium-ion batteries [30, 47, 86] and for reversible energy storage.[87, 88]
Hexaferrite compounds are of interest from both the theoretical and practical standpoints. Determination of the physicochemical grounds for the synthesis and operation of hexaferrite type HEOs was addressed by Zaitseva,[89] who described the synthesis and thermodynamic properties of these compounds, studied the structure of samples, and measured the magnetic and electrophysical characteristics. It was found that elements such as Fe, Al, Ba, Sr, Co, Cr, Ga, and In tend to be incorporated into M-type hexaferrite HEOs; Ca, Cu, Ni, Sn, Zn, Zr, La, V, Pb, Mn, and Ti have limited solubility; and Bi, K, and W have low solubility. The study of magnetic and electrodynamic properties revealed weakening of the main magnetic characteristics and a marked decrease in the DC conductivity and dielectric losses following the replacement of iron by some ions such as Al3+, In3+, Ga3+, and Ti4+. The observed set of properties makes M-type hexaferrite HEOs promising materials for components of ultra-high-frequency devices.
It is promising to use REEs in HEOs. Keneshova et al.[45] showed that it is of interest to study the structure and electrodynamic properties of the high-entropy REE-containing Sm – Ce – Gd – Sc–A – O oxide system, where A is La, Y, Er, Ho, Yb, Nd. It was found by powder X-ray diffraction that compounds that are formed in the Sm – Ce – Gd – Sc – Yb – O system crystallize in the cubic system identical to the crystal structure of Sm2O3, with the compounds formed in this system being dielectrics.
High-entropy hydroxides based on the Al – Fe – Cr – Ga system containing one of In, Er, Ho, Y or Ce cations can also serve as adapted HEO precursors.[90] The authors illustrated potential ways of using these hydroxides as catalysts and ceramic powders.
The properties of high-entropy borides formed in the Hf – Mo – Nb – Ta – Ti – B and Hf – Mo – Nb – Ta – Zr – B systems at high pressures and high temperatures were reported by Iwan et al.[91] It was shown that the high-entropy borides are stable at a pressure of 9.5 GPa and a temperature of 2273 K. The high compressive strength and phase stability of high-entropy borides at high pressures and high temperatures make them perfect candidates for construction materials in nuclear and aerospace applications.
3. High-entropy carbide systems
High-entropy carbides containing several metals, unlike the traditional carbides containing one or two metals, exist as a variety of compositions possessing unusual and promising properties.[15] Multicomponent carbides are based on carbon and group 4 and 5 transition metals, the atoms of which present in equimolar ratio form a cubic crystal lattice. The single-phase carbides in which all metal atoms are uniformly distributed throughout the crystal have unique mechanical properties, high melting point, low thermal conductivity, increased hardness, resistance to mechanical fractures, and thermal stability.
Since carbide-based materials are stable to very high temperatures above 2773 K, they are fairly promising for the manufacture of refractory ceramics and further use in industrial catalysis.[17] The high-temperature mechanical properties of HECs are of interest since they are often used in high-temperature environments. It is necessary to emphasize that the high-temperature flexural strength of the high-entropy carbide (Hf0.2Zr0.2Ti0.2Ta0.2Nb0.2)C and the Ti – Ta – Zr – Nb – C system retains their room-temperature value of 300 – 500 MPa up to approximately 1873 – 2073 K, i.e., these materials demonstrate a better retention of strength characteristics than some typical mono-, binary, and ternary carbides.[17]
In relation to Ti – Zr – Nb – Hf–Ta – C high-entropy carbides, Nikitin et al.[92] demonstrated that the plasma dynamic technique using the high-speed arc discharge plasma jet is among the optimal methods for their synthesis.
It should be emphasized that development of a procedure for predicting the compositions and properties of HECs is a highly relevant problem. Below we consider some approaches currently available for solving this problem. Sarker et al.[93] developed a method that was applied to disordered refractory carbides based on five metals, promising candidates for the fabrication of high-hardness materials. The proposed calculation method makes it possible to design entropy-stabilized HEMs. Using this method, Harrington et al.[94] reported the composition (V0.2Nb0.2Ta0.2Mo0.2W0.2)C, which appears to be a probable candidate for further studies as entropy-stabilized carbene.
Rempel and co-workers [95] investigated the six-component high-entropy carbide (Ti0.2Zr0.2Hf0.2Nb0.2Ta0.2)C. The electronic structure was calculated using the ab initio VASP package for a 512-atomic supercell built using special quasi-random structures. Using the electronic structure and deep machine learning, an interatomic neural network potential was generated, which allowed calculation of the structural and mechanical characteristics of the (Ti0.2Zr0.2Hf0.2Nb0.2Ta0.2)C high-entropy carbide. The calculated and experimental values were in good agreement.
Liu et al.[96] illustrated the possibility of predicting new HECs based on group 4 and group 5 refractory metals (Ti, Zr, Hf, V, Nb, Ta) possessing high hardness and high melting points on the basis of thermodynamic approach. The results of calculations performed for fifteen systems, six of which were synthesized experimentally, unambiguously demonstrated the phase stability of ceramic materials (Fig. 7). For all of the fifteen carbide systems, the energies of formation (Fig. 7a) were negative and the enthalpies of mixing (Fig. 7b) were positive, but for most of the carbides, these values were moderate.
Multicomponent carbides have been studied to a much lesser extent than HEOs. However, research related to HECs is now being actively pursued. The following studies should be mentioned in this respect. The synthesis,[97-105] mechanical [94, 106-108] and thermal properties,[109-114] as well as the chemical oxidation [115-118] and corrosion [15, 42, 117] resistance of HECs have been studied in detail. Demirskyi et al.[108] determined the flexural strength of (TaZrNb)C3 in the temperature range of 298 – 2273 K, while Feng et al.[109] obtained the corresponding temperature dependence for (HfZrTiTaNb)C5 in the 298 – 2573 K temperature range. The mechanism of oxidation of high-entropy carbides was studied by Yudin et al.[116]
The ultra-high-temperature HEC (TiNbTaZrHf)C5 was successfully synthesized via an electrochemical process, which opened up a new approach to the synthesis of other entropy-stabilized materials.[119]
Pak et al.[120] developed a controlled synthesis of the HEC (TiZrNbHfTa)C5, which was based on the preliminary canonical Monte Carlo simulation using interatomic potentials for machine learning to determine the temperature conditions for the formation of single-phase and multiphase samples. It was shown that the formation of single-phase HEC samples requires high synthesis temperatures of more than 1773 K, while at lower temperatures, the synthesis gives multicomponent HEC samples in which two or more different phases coexist. In full agreement with the calculations, a single-phase sample was successfully obtained using arc discharge at a temperature of 2000 K. At temperatures below 1200 K, the TiZrNbHfTaC5 sample degraded into components of the Ti – Nb – Ta – C system and mixtures of components of the Zr – Hf–Ta – C, Zr – Nb – Hf – C, Zr – Nb – C, and Zr – Ta – C systems.
It has been repeatedly shown that the properties of the resulting single-phase solid solutions, important for practical use, depend on the stoichiometry. The microstructure of HEC (TiZrNbHfTa)C5 prepared by vacuum-free electric arc method has been studied.[121, 122] A solid solution with a cubic lattice was obtained upon the synthesis and the lattice parameters were determined; the solid solution contained simultaneously titanium, zirconium, niobium, hafnium, tantalum, and carbon atoms.
Ma et al.[123] synthesized transition metal-based HECs (Zr0.25Hf0.25Ta0.25Nb0.25)C and (Zr0.25Hf0.25Ta0.25Ti0.25)C with adjustable carbon stoichiometry; the products were single-phase solid solutions with controlled mechanical properties. The effect of the nature of transition metals on the phase stability in the Zr – Nb – Ta – C, Zr – Nb – Ta – Hf – C, Zr – Nb – Ta – Hf – Ti – C, and Zr – Nb – Ta – Hf – Ti – V – C systems, which formed one rock salt phase, was studied by Yan et al.[124] A study of high-entropy ceramics based on the Ta – Hf – Zr – Nb – C system [125-127] revealed higher creep resistance compared to that of monocarbides; in the authors’ opinion, this may be attributable to a crystal structure distortion and a higher thermodynamic stability of the ceramics at high temperatures.
Braic and co-workers,[42, 125, 126] who investigated the biocompatibility and corrosion resistance in simulated biological fluids, demonstrated benefits of using multicomponent carbides as biocompatible coatings for medical applications.
The number of works addressing thermodynamic properties of HECs is moderate,[127-129] with most of them dealing with ab initio calculations. Jiang et al.[128] calculated the temperature dependences of entropy, heat capacity, and thermal expansion coefficient for Hf – Ta – Zr – Ti – C and Hf – Ta – Zr – Nb – C HECs in the temperature range of 0 – 2000 K. Previously,[129] the electronic structure, mechanical properties, and thermal stability of (TiZrHfNbTa)C5 were calculated in the temperature range of 0 – 1670 K. Zhou et al.[97] used spark plasma sintering to synthesize an equiatomic powder based on high-entropy Ti – Zr – Hf – Nb – Ta – C carbide and showed that a solid solution with a face-centred cubic lattice could be obtained at 2223 K. The powder had better oxidation and thermal stability than the starting components.
It should be noted that no results of experimental determination of thermodynamic properties of multicomponent carbides have been reported as yet. Thus, it is obvious that experimental measurements of physicochemical properties, including thermodynamic properties, of HECs is now an important area of physicochemical studies, especially in view of the potential use of multicomponent carbides in the development of highly refractory materials.
4. High-entropy oxycarbide systems
The logical continuation of the studies of high-entropy oxides and carbides is switching to multicomponent high-entropy oxycarbides (HECOs). Analysis of relevant publications indicates that this area is at an early stage of development. There is only one publication [18] demonstrating the possibility of obtaining single-phase oxycarbide (Hf0.25Zr0.25Nb0.25Ti0.25)(C0.5O0.5).
The authors of that study noted that compositionally complex ceramics are promising for the fabrication of highly stable materials, which are in demand for operation under extreme environmental impacts, including harsh conditions of high-temperature oxidation and corrosion. This was confirmed by the data (Fig. 8a) indicating that the oxycarbide sample (Hf0.25Zr0.25Nb0.25Ti0.25)(C0.5O0.5) (HECO) had higher initial oxidation temperature and a lower oxidation rate compared to those of the corresponding carbide sample (Hf0.25Zr0.25Nb0.25Ti0.25)C (HEC).
The authors interpreted the results of testing of carbide HEC and oxycarbide HECO samples by calculating the thermodynamic functions for the carbide and oxycarbide oxidation reactions using density functional theory (DFT) ab initio calculations (Fig. 8b). In this regard, there is no doubt about the expediency of studying the thermodynamic properties of HECOs, which are in great demand for analysis of the conditions of synthesis and operation of the corresponding materials. In view of the possibility of using these materials as ultra-high-temperature ceramics, data on HECO vaporization are also of considerable interest for predicting the high-temperature behaviour of these systems under extreme temperature conditions.
High-entropy carbides and oxycarbides showed increased thermal and chemical stability; therefore, they can be used to develop new types of ultra-high-temperature ceramics, including new-generation thermal barrier protective coatings,[17, 18] which are in demand for aviation and aerospace engineering. The oxidation and corrosion resistance of multicomponent carbides [39, 43, 118] and oxycarbides [18] is not only useful for the development of materials for critical applications that should retain the service properties under extreme environmental impacts. Furthermore, in combination with the biocompatibility of these compounds,[42, 125, 126] this makes them applicable for the design of modern biomedical coatings for implants.[12] It was shown [18, 43] that oxycarbide phases are chemically more inert to high-temperature oxidation with oxygen than the corresponding carbides; hence HECOs can be recommended as the optimal and the most promising highly refractory material candidates.
Currently, the operation of HEO-based materials at high temperatures has certain limitations because of unstable operation, especially in a reducing atmosphere during repeated heating – cooling cycles. For this reason, HECs and HECOs, known for the resistance to high-temperature impacts,[18, 130] are of particular interest for considering the effect of a reducing environment on the physicochemical properties of HEMs.
As shown convincingly in reviews addressing the physicochemical properties of oxide and carbide systems,[12, 13, 15] today there is virtually no information on the high-temperature thermodynamic characteristics even for the most studied high-entropy oxide systems. Analysis of the available literature on the high-temperature behaviour of multicomponent systems also indicates the lack of data on the vaporization of high-entropy oxides and carbides.[130, 131]
The limited information on the vaporization processes and thermodynamic properties of the considered systems at high temperatures substantially complicates their stable operation under extreme temperature conditions.
That is why the final part of this review focuses on the currently available data on the physicochemical properties of binary and multicomponent systems, which could potentially be of interest for the fabrication of multicomponent high-entropy systems stable at high
5. Thermodynamic aspects of the stability of high-entropy compounds and materials based on oxides, carbides, and oxycarbides
The main goal of the design of high-entropy materials stable to high-temperature impacts is to expand the limiting number of components in a single-phase solid in order to attain unique and tunable properties. Due to the considerable interest and numerous studies aimed at the development of new materials based on oxides, carbides, and oxycarbides, many authors turn to the fundamental thermodynamic approaches within the constraints that would determine the structure of future HEMs.[48]
The main thermodynamic condition for the formation and stability of HEMs consisting of five and more elements present in equatomic proportions (most often, 5 – 35 mol.%) is the magnitude of configurational entropy of no less than 1.609R per mole.[48]
The total entropy S of oxides includes several components such as atomic vibrational SA, magnetic SB, and configurational SC entropy components:[7]
The greatest contribution to the total entropy is made by the configurational entropy depending on the atom arrangement.[56] It was shown [5, 56] that the ideal configurational entropy ΔSconf has the form
where R = 8.314 J mol–1 K–1, R is the universal gas constant, xi is the mole fraction of the i-th component in the mixture, N is the number of components (present in the equimolar amounts).
The configurational entropy is a function of the number of components and increases as the number of components increases. The data shown in Fig. 9 illustrate the configurational entropy equal to 0.693 R per mole for two components, 1.609 R per mole for five components, and 2.303 R per mole for ten components. Thus, the addition of more components continues to increase the total configurational entropy, but the effect becomes less pronounced with a greater number of components (see Fig. 9).
The multicomponent equiatomic systems are usually subdivided into three types in terms of entropy: low-, medium-, and high-entropy systems. According to this classification, if the number of components in an equiatomic system is five or more, it can be assigned to the class of HEMs.
In the case of oxides, Eqn (2) for the configurational entropy of ideal mixing includes the second sum over sublattices [7, 48] and is given by
where ms is the multiplicity of sublattice s, and xi,s is the mole fraction of element i on sublattice s.
This modification explains the potential contribution to the overall configurational entropy arising due to multiple cation sublattices, oxygen vacancies, or other forms of disorder in the anion sublattice.[7] The effect of the configurational entropy on the stability of multicomponent oxides has been analyzed.[7, 48]
The concept of entropy-stabilized ternary oxides was first developed [132-135] almost 50 years ago and was used to consider the formation of spinels [132-135] and pseudobrookite.[136] It was shown that in both cases, the configurational entropy of the disordered cation distribution exceeds, at a certain temperature, the positive enthalpy of formation of the compounds from pure oxides. Below this temperature, both groups of single-phase ternary oxides degraded into a mixture of binary oxides. Thus, the critical temperature determines the competition between the enthalpy and entropy contributions.
The homogeneous single-phase HEOs are stable if the positive entropy of formation of these compounds is sufficiently high to counterbalance the enthalpy of formation above some critical temperature; this results in a negative Gibbs free energy above the critical temperature [7] according to the equation
where ΔG, ΔH, and ∆S are the changes in the Gibbs energy, enthalpy, and entropy, respectively; T is the absolute temperature, K.
Thus, the key thermodynamic condition for the formation and stability of single-phase entropy-stabilized HEOs is a high configurational entropy, a low heat of formation, and a critical temperature, which determines the interplay between the enthalpy and entropy contributions.
A series of calculations of the Gibbs energy using the regular solution model performed for a single-phase solid solution [48] at various temperatures is depicted in Fig. 10.
Examination of the dependences of thermodynamic properties on the composition of the condensed phase shown in Fig. 10 unambiguously indicates that in the case of entropy-stabilized solid solution (Fig. 10a), the major contribution to the negative Gibbs energy is made by the term –TΔSmix. In the case of the enthalpy-destabilized solid solution (Fig. 10b), the +ΔHmix and –TΔSmix terms are similar. In this case, the overall Gibbs energies of formation attest to the presence of two saddle points with different compositions of the condensed phase. Despite the fact that the Gibbs energy of formation of this system is negative over the whole range of compositions, phase separation is observed. As a larger number of components is added, the probability of system stabilization owing to increase in the entropy contribution increases.
As noted in the cited paters,[7, 48] the key mechanisms of the phase stability of complex multicomponent HEOs can be very different, especially in the presence of strong electrostatic interactions and ionic and covalent bonds and also in those cases where different crystal structures are formed or the same structure is formed at various compositions of the condensed phase of the system.
While considering the fundamentals of the existence of thermodynamic equilibrium, McCormack and Navrotsky [48] demonstrated that it is the change in the chemical potential of a component that determines the stability of a solid solution upon addition of a new component. In the case of ideal mixing, the solid solution stability is dictated by the configurational entropy, while in the case of non-ideal mixing, the stability is affected by numerous factors. These factors include characteristics of the transitions between various structures, surface effects, structural defects, and other parameters that can affect the enthalpy and entropy changes. The authors [48] showed that the type of components and the mode of their interaction are more significant for the stability of the system as a whole than the number of components. Non-ideal mixing is the key condition for stabilization and destabilization of solid solutions. The change in the chemical potential of a component determines the phase stability. Let us recall the relations characterizing the change in the chemical potential of a component (Δμi) in the case of ideal mixing,
where xi is the mole fraction of the i-th component in the mixture. In the case of non-ideal mixing,
It is noteworthy that ΔGEi and ΔSEi depend on the type of components, composition of the solid solution before the new component has been added, and the properties of the new component.
To summarize the discussion about the significance of the thermodynamic approach for the development of HEMs, it is necessary to pay attention to the major criteria of HEO stability proposed in the literature [7, 48, 56]
— the simplest HEO consisting of isostructural components with equal ion size and valence is stabilized only by the entropy of mixing (–TΔSmix) that is greater than the positive enthalpy of mixing (ΔHmix), which results in a negative Gibbs energy ΔGmix < 0. These HEOs would be stable only above the critical temperature and become unstable at low temperatures;
— when there are strong electrostatic interactions, oxide systems tend to form more stable compounds at lower temperatures;
— owing to ionic and covalent bonds, ordering in oxides is the norm rather than an exception. Both the short- and long-range order existing in the solid phase decreases the overall contribution of the configurational entropy upon mixing. Thus, HEOs can have high entropy only if they are disordered at high temperatures;
— not only the number of components, but also the types of components and the way they interact affect the stability of a solid solution. The effect of non-ideal mixing is a key condition in the stabilization and destabilization of solid solutions.
It is noteworthy that despite the above-stated results of studies of high-entropy compounds aimed at the development of materials with unique physicochemical properties, there is also an alternative point of view. In particular, it was noted [137] that, at least in real practically significant metallic systems, strong interaction between the components always predominates and decreases the entropy. Meanwhile, in multicomponent systems in which the interactions between the components are weak and the entropy factor predominates, one can hardly expect the appearance of new unique properties, and this significantly reduces the benefits of such multicomponent systems. The authors [137] draw a conclusion that high-entropy systems are indeed promising for the development of new materials with unexpected properties; however, these properties do not arise due to configurational entropy but are related to other effects.
Thus, the key criteria outlined in this Section should be taken into account in the design and synthesis of new HEMs. However, one should also bear in mind the data [7, 48, 56, 137] indicating that the driving force of formation of high-entropy solid solutions is not always strictly entropy-controlled and that the properties arising due to the ‘cocktail effect’ can actually be caused by non-ideal mixing.
6. Experimental methods for investigation of high-entropy oxide, carbide, and oxycarbide systems at high temperatures
It is known that the traditional experimental methods that are now used to study the thermal stability of oxide-, carbide-, and oxycarbide-based HEMs include thermogravimetry, differential scanning calorimetry (DSC), thermomechanical method, and Knudsen effusion mass spectrometry, or high-temperature mass spectrometry method. We will briefly note the main features and advantages of the listed experimental approaches for high-temperature studies.
Thermogravimetry is the most popular high-temperature method used to study the vaporization processes and phase equilibria of HEMs; the essence of the method is continuous measurement of the sample mass loss during controlled variation of the temperature.[138]
Differential scanning calorimetry [139, 140] implies measuring the amounts of heat absorbed or released by a sample during controlled temperature variation. The advantages of this method include the possibility of determining the temperature ranges and heats of phase transitions and heat capacities of compounds in a specified temperature range. In certain cases, thermogravimetry and DSC are successfully combined in the same instrument for simultaneous thermal analysis, which provides more correct description of the processes that take place in the sample during heating.
The thermomechanical method is an alternative version of DSC supplemented by determination of the change in the sample size or volume during the controlled temperature variation.[141]
The Knudsen effusion mass spectrometry, or high-temperature mass spectrometric method is a unique approach of high-temperature materials science, which makes it possible to study vaporization processes and thermodynamic properties of low-volatile substances at temperatures up to 3000 K.[142-146] The combination of the classical Knudsen method for determining the total vapour pressure and mass spectrometric analysis of the gas phase enables not only identification of vapour species over the samples, but also determination of the thermodynamic functions (partial pressures of vapour species, activities of components, Gibbs energy of formation, excess Gibbs energy, enthalpies of vaporization, and enthalpies of mixing).[142-146]
6.1. Multicomponent oxide systems
The considerable progress of high-temperature mass spectrometry in the studies of binary and multicomponent oxide systems over the past 50 years [131, 143, 147-157] resulted in the development of acid – base concept of vaporization of oxide systems,[152, 154] which is able to predict the most probable vaporization processes of the components upon temperature rise to 3000 K. It was shown[131, 143, 147-157] that processes that may take place in the vapour over multicomponent oxide systems at high temperatures include dissociation, association, polymerization, and vaporization without changes in the molecular species. For example, considering the tendency towards dissociative vaporization of the corresponding oxides,[149, 150] we assumed that atomic iron is selectively vaporized from fairly promising high-entropy compound (Sr0.67La0.33)(Ti0.33Zr0.33Fe0.33)O3 (SrO : La2O3 : TiO2 : ZrO2 : Fe2O3 = 0.40 : 0.10 : 0.20 : 0.20 : 0.10 mole fractions). Study of the vaporization of this compound by Knudsen effusion mass spectrometry [158, 159] at 1720 K actually demonstrated considerable selective vaporization of atomic iron as a result of dissociative transition of iron oxide to the gas phase (Fig. 11). As follows from this example, the thermal stability of HEOs under high-temperature operation conditions is largely limited by the nature of the most volatile components that are prone to selective vaporization and, in this particular case, it is limited by a temperature of 1720 K.
6.2. Multicomponent carbide systems
The processes of vaporization and thermodynamic properties of single carbides, which have been studied mainly by high-temperature mass spectrometry, are integrated and systematically arranged by Kazenas and Tsvetkov.[160] The vaporization of carbides, particularly SrC2, LaC2, La2C3, TiC, ZrC, and HfC, is most often accompanied by dissociation to the corresponding atoms and, to a lesser extent, by the formation of more complex molecules.[160] Today, study of vaporization processes and thermodynamic properties of multicomponent carbide systems at high temperatures is virtually limited to the results reported by Vorozhtcov et al.[161] (Table 2).
Heating of the carbides Al4C3 , Ti2AlC, Ti3AlC2 , Zr2AlC, and Zr3AlC2 to 1500 K was accompanied by selective vaporization of atomic aluminium, whereas titanium, zirconium, and carbon remained in the condensed phase. As the temperature was raised to 1870 K, atomic titanium and zirconium appeared in the gas phase over the МAХ phases, while vaporization of carbon was noted only at temperatures above 2300 K. The gas phase over SiC, Ti2SiC, and Ti3SiC2 was found to contain Si, Si2 , SiC2 , and Si2C species at temperatures above 1900 K. This made it possible to determine the temperature dependences of the partial pressures of the vapour species identified over carbide ceramic samples and to identify the least volatile (the most thermally stable) carbides.
As a result, it was established that the total pressure of the vapour species Si, Si2 , SiC2 , and Si2C increases in the following order of silicon-containing carbide systems: Ti2SiC < Ti3SiC2 < SiC. Over the carbide systems containing aluminium, the partial pressure of atomic aluminium in the vapour increases in the following series: Zr2AlC < Zr3AlC2 < Ti2AlC < Ti3AlC2 .[161]
Meanwhile, Simonenko et al.[162, 163] successfully used Ti2AlC and Ti3AlC2 as sintering additives to decrease the consolidation temperatures of a number of ultra-high-temperature compounds based on zirconium and hafnium diborides and carbides in the HfB2 – SiC and Ta4HfC5 – SiC systems in the reactive hot pressing and spark plasma sintering. This enabled the production of unique ultra-high-temperature ceramic materials based on the HfB2 – SiC system for high-speed flight vehicles, which were stable on laser heating up to a temperature of 2473 K when operating in a CO2 atmosphere similar in composition to the Venus and Mars atmospheres.[163] The possibility of stable operation of a ceramic material containing Ta4HfC5 and 30 vol.% SiC at temperatures above 2027 K in a supersonic nitrogen flow was established.[164]
Sheindlin et al.[165] synthesized for the first time HECs (HfTaNbZr)C and (HfTaTiNbZr)C with a solidus temperature of approximately 4000 K by the carbothermal reduction of a mixture of the corresponding oxides followed by compaction in a spark plasma sintering furnace; the authors determined the heat capacity, thermal expansion, thermal conductivity, and emissivity of these compounds at temperatures above 3000 K.
6.3. Multicomponent oxycarbide systems
Currently, information on the high-temperature behaviour of even single oxycarbides is rather limited; that is why, first we will pay attention to the available data concerning the most studied oxycarbides in the Ti – C – O, Zr – C – O, and Hf – C – O systems, which form solid solutions based on titanium, zirconium, and hafnium oxycarbides with the cubic structure.
The phase diagram of the Ti – C – O system includes equilibria for the solid solutions identified previously in binary systems; no new compounds have been found in the ternary system. The phase equilibria in the Ti – C – O system were studied experimentally in a few works.[166-168] It was shown that the cubic δ-phases TiOx and TiCx in two binary systems form a continuous series of δ-TiCxOy solid solutions in this system over a broad temperature range of 1073 – 2020 K.[169] The liquidus of the Ti – C – O system was also optimized on the basis of experimental data.[169]
The increasing interest particularly in the δ-phase of the Ti – C – O system is due to the emerging prospects of using this phase as a consumable anode for the electrolysis in salt melts to obtain high-purity titanium.[170, 171] For this reason, the thermodynamic properties of phases in the Ti – C – O system, especially the δ-TiCxOy phase, have been repeatedly studied, but not using high-temperature mass spectrometry. For example, the enthalpies of formation of some samples in this solid solution at 298 K were determined by combustion calorimetry.[172] Ouensanga [173, 174] investigated the reduction of rutile with carbon in a CO atmosphere. The partial pressures of carbon monoxide occurring in equilibrium with the TiCxOy – C system were measured in the temperature range of 1400 – 1600 K. The resulting temperature dependences of the CO partial pressures over TiCxOy were used to determine the activities of titanium in the oxycarbide phase and the Gibbs energies of formation of TiCxO1 – х, where х = 0.67 – 1.00, at 1580 K. In the solid solutions of the TiC – TiO quasi-binary system, negative deviations from the ideal behaviour were observed.[173, 174]
The heat capacity of TiC0.5O0.5 was measured by DSC in the temperature range of 373 – 1273 K, which made it possible to determine the enthalpy of mixing and the Gibbs energy of mixing of the indicated solid solution.[175] The heat capacities of TiC0.5O0.5 were optimized and shown to obey the Neumann–Kopp rule. The presence and the number of vacancies in the crystal structure of TiCxOy were studied experimentally.[176] Experimental and theoretical determination of the thermodynamic properties of the TiC1 – xOx solid solution (0 ≤ x ≤ 1) was reported.[177] The enthalpies of combustion of samples of this solid solution in an oxygen bomb calorimeter were determined. On the basis of the results, the enthalpies of mixing were found, which were in line with the results of DFT quantum chemical calculations. The authors analyzed the relationship between the thermodynamic properties and the structural characteristics of the TiC1 – xOx solid solution, in particular the mechanism of vacancy formation in the Ti – C – O system.[177]
The phase diagram of the Zr – C – O system was optimized [178] using the CALPHAD approach in the temperature range of 1923 – 2273 K, and later calculated [179] using the NUCLEA database.[180] A fundamental difference between the Zr – C – O phase diagram and the Ti – C – O phase diagram considered above is that the ZrC1 – x-based solid solution has a limited concentration range of homogeneity, unlike the TiCx-based solid solution, which has a continuous homogeneity region extending from one (Ti – C) to the other (Ti – O) binary system.
Gendre et al.[181] investigated the mechanical properties of oxycarbide Zr – C – O solid solutions synthesized by carbothermal reduction; they measured the Young modulus, porosity, and the average size of crystal grains, which were on average 5 μm. Pipon et al.[182] investigated the diffusion of xenon in zirconium oxycarbides ZrCхOу at high temperature as a function of the oxygen content in the solid solution. It was shown that a decrease in the oxygen content makes the material more impermeable for xenon. This opens up the prospects of using zirconium oxycarbide with low oxygen content (not more than 8 at.%) as a fuel rod cladding material for gas-cooled fast reactors in order to prevent emissions of xenon, which is one of the fission products.
The possibility of using zirconium oxycarbide ZrO0.31C0.69 as a catalyst in electrochemical energy conversion reactions was also considered.[183] For this purpose, the stability of nano-sized ZrO0.31C0.69 powder in atmosphere of various gases at temperatures of 298 – 1073 K was studied by X-ray diffraction and impedance spectroscopy. It was shown that ZrO0.31C0.69 is stable when heated in a reducing atmosphere (hydrogen, methane), but decomposes in an oxygen or carbon dioxide atmosphere. The hydrogen, carbon dioxide, and oxygen overpotentials were determined. The applicability of ZrO0.31C0.69 as a catalyst for electrochemical reactions, e.g., anode oxidation of alcohols, was demonstrated.[183]
The phase diagram of the Hf – C – O system, similarly to that of the Zr – C – O system, was optimized [184] by the CALPHAD approach in the temperature range of 1923 – 2023 K. The concentration boundaries of the HfCхOу solid solution were determined. It was shown that the oxygen content in this solid solution does not exceed 10 at.% at 1923 K (homogeneity region up to HfC0.90O0.10); temperature rise does not lead to extension of the homogeneity region, as opposed to the Zr – C – O system in which the homogeneity region of the ZrCхOу solid solution is expanded with temperature rise. No new compounds containing simultaneously hafnium, oxygen, and carbon have been found in the Hf – C – O system.[184]
The enthalpies of formation of HfCхOу were determined [185] by the combustion calorimetry in the 0.592 ≤ x ≤ 0.982; 0.006 ≤ y ≤0.149 concentrated ranges and approximated by an empirical equation as functions of х and у.
Among oxycarbide systems, the La2O3 – C – LaC2 system was studied by high-temperature mass spectrometry;[186] the partial pressures of CO in the vapour over this system in the temperature range of 1343 – 1638 K were found and used to calculate the enthalpies and the Gibbs energies of formation of the solid lanthanum dicarbide LaC2 at 298 K.
A series of studies [43, 161, 187, 188] describes for the first time the synthesis and study of not only carbide ceramics based on the Ti – Si – C, Ti – Al – C, and Zr – Al – C systems according to the stoichiometry of МAХ phases, Ti2SiC (Ti2AlC, Zr2AlC) and Ti3SiC2 (Ti3AlC2 , Zr3AlC2), as noted above, but also oxycarbide ceramics based on the indicated МAХ phases with zirconium and hafnium oxides.
The high-temperature behaviour of the obtained ceramics was investigated by DTA and the heat capacities were measured by DSC.[43] The vaporization processes and thermodynamic properties of the oxycarbides Ti2AlC – HfO2 and Ti3AlC2 – HfO2 were investigated by high-temperature mass spectrometry using graphite effusion cells.[161, 188] The vapour over the oxycarbide Ti2AlC – HfO2 , Ti3AlC2 – HfO2 , Zr2AlC – HfO2 , and Zr3AlC2 – HfO2 systems was found to contain, apart from atomic aluminium, also Al2O, which was not detected in the gas phase over МAХ phases. Similarly, the SiO vapour species, which was not characteristic of the corresponding carbide vaporization, was identified in the vapour over the Ti2SiC – HfO2 and Ti3SiC2 – HfO2 systems. Thus, Vorozhtcov and co-workers [161, 188] established for the first time the temperature limits of the thermal stability of the systems of МAХ phases with HfO2 (see Table 2).
To conclude this Section, we would like to pay attention to the exceptional capabilities of the high-temperature mass spectrometry for determination of the enthalpy of mixing of binary and multicomponent systems at high temperatures considering the FeO – TiO2 system as an example (Fig. 12).[189]
As indicated by the modest amount of data presented in this Section, study of the thermal stability, phase equilibria, and thermodynamic properties of multicomponent carbide and oxycarbide systems to be used for the synthesis and modelling of the physicochemical properties of high-entropy compounds is now a fairly significant problem.
7. Model approaches to the study and prediction of thermodynamic properties and phase equilibria
of high-entropy compounds and materials based on oxides, carbides, and oxycarbides at high temperatures
The high-temperature experimental studies of thermodynamic properties, especially mass-spectrometric studies, and experimental studies of the phase equilibria in multicomponent oxide, carbide, and oxycarbide systems are highly labourious. Therefore, in recent decades, thermodynamic calculations of high-temperature equilibria using computer simulation have been actively developed all over the world. Data on the thermodynamic properties of these systems gained using model approaches can serve to predict the most important physicochemical characteristics of materials under specified conditions and thus substantially reduce the scope of experimental work. Correct use of thermodynamic information in the calculations requires application of model approaches to coordinate and interpolate the array of experimental data obtained for the given system.[190] It is noteworthy that issues of modelling of phase equilibria and thermodynamic properties in high-entropy systems currently receive considerable interest in the world literature.[191-195] For example, a model has been proposed for the description of thermodynamic properties of hexaferrite type high-entropy oxides for the development of the theoretical fundamentals of the solid-phase synthesis of HEOs.[195]
In the last decades, this problem has been mainly addressed using the CALPHAD approach.[196, 197] According to the CALPHAD approach, all available thermodynamic values and data on phase equilibria in the system are optimized together to obtain one consistent set of model equations for the Gibbs energy that best reproduces the known data for all phases of the system as functions of temperature and component contents (Fig. 13).[190, 198] In this case, thermodynamic data for binary systems determined in this way can be used for further prediction of the thermodynamic properties and phase equilibria in higher-order systems.
Since the end of the 1970s, for successful implementation of the CALPHAD approach to calculate phase equilibria at high temperatures, various databases were formed and have been widely used, e.g., ThermoCalc,[199] FactSage,[200] SGTE,[201] and NUCLEA [180, 202] databases containing the optimized information about the phase equilibria and thermodynamic properties of a broad range of systems.
The capabilities of one database, NUCLEA,[180] were illustrated in relation to systems that can potentially be constituents (parts) of high-entropy compounds. The NUCLEA database [180, 202] was developed for optimization and calculation of thermodynamic properties and phase equilibria in the systems that are of interest for considering processes in nuclear reactors. The program package based on the NUCLEA database and the GEMINI2 Gibbs energy minimizer [180] can be used to perform the thermodynamic calculations of the phase equilibria in multicomponent systems that are of interest for analysis of in-vessel and ex-vessel stages of severe accidents at nuclear power plants. The NUCLEA database combines the results of experimental studies of the phase equilibria and thermodynamic functions for more than four hundred binary and ternary systems based on eighteen elements: O, U, Zr, Ag, In, B, C, Fe, Cr, Ni, Ba, La, Sr, Ru, Al, Ca, Mg, and Si. The experimental high-temperature data available for the indicated systems were optimized and presented as self-consistent phase diagrams of the systems and as concentration and temperature dependences of the Gibbs energy for all phases of the system. The use of the GEMINI2 Gibbs energy minimizer makes it possible to extrapolate the Gibbs energies that were used in the database development to the studies of multicomponent systems. The calculation of phase equilibria involves modelling of the Gibbs energy for the sets of all phases, compounds, and solutions that may exist in the system under study. The thermodynamically equilibrium set of coexisting phases under specified conditions is found by minimization of the total Gibbs energy of the system provided that the external pressure is constant.
The extensive capabilities of the NUCLEA database were illustrated by calculating the phase equilibria for the Al2O3 – SiO2 – ZrO2 [203, 204] and La2O3 – SrO – ZrO2 systems up to 3000 K and Zr – C – O [179] system up to 4900 K.
Vorozhtcov et al.[203] used the NUCLEA database and the GEMINI2 software to perform thermodynamic modelling of the phase equilibria in the Al2O3 – SiO2 – ZrO2 system in the temperature range of 400 – 2550 K. The calculated eight isothermal sections of the phase diagram of this system supplemented the scarce experimental data obtained previously.
The materials based on the multicomponent Al2O3 – SiO2 –ZrO2 glass ceramic system are of considerable interest for the development of optimal and relevant solutions in various fields of modern engineering, in particular, refractory and protective coating technologies for heat-resistant metallic materials. That is why the data on phase equilibria in the Al2O3 – SiO2 – ZrO2 system calculated for the first time are of considerable interest.[203]
As an example, Fig. 14 compares the isothermal sections of the Al2O3 – SiO2 – ZrO2 phase diagram calculated using the NUCLEA database for temperatures of 1900 and 1910 K. The calculation results indicate (Fig. 14a) that at 1900 K, the concentration ranges of the phase fields involving zircon decrease, while upon the temperature rise to 1910 K (Fig. 14b), ZrSiO4 completely decomposes.
Thus, as indicated by Vorozhtcov et al.,[203] comparison of the results of phase diagram modelling for the Al2O3 – SiO2 – ZrO2 system up to a temperature of 2550.15 K with available experimental data for the ternary [205, 206] and corresponding binary systems shows only some agreement between the experimental and calculated values. Therefore, it seems reasonable to carry out both further modification of experimental methods used to study phase equilibria and updating of the NUCLEA database [180, 202] by adding a larger number of new reliable thermodynamic data for a wider range of chemical elements with the involvement of modern physicochemical models to predict the phase equilibria.
The La2O3 – SrO – ZrO2 system is a promising base for high-temperature ceramics and materials with unique optical, electrochemical, and catalytic properties. The absence of published data on the phase equilibria in the La2O3 – SrO – ZrO2 ternary system accounted for the application of the NUCLEA database to predict them.[207] The reliability of the data on the phase equilibria in the La2O3 – SrO – ZrO2 system was discussed resorting to the available information on the corresponding binary systems. The authors also compared the results of simulation of the phase diagram for the SrO – ZrO2 system with the available experimental data.
It is noteworthy that the phase diagram of the SrO – ZrO2 system accepted after the NUCLEA optimization differed substantially from that reported in the most trustworthy study by Gong et al.[208] in both the number of compounds formed in the system and the formation and melting temperatures of Sr3Zr2O7 (Fig. 15). According to the calculations using the NUCLEA database, Sr3Zr2O7 is formed at 2289 K upon the reaction of SrZrO3 with Sr2ZrO4; however, this was not confirmed by Gong et al.,[208] who experimentally illustrated the stability of Sr3Zr2O7 at lower temperatures. According to the NUCLEA data, Sr2ZrO4 and Sr3Zr2O7 melt incongruently at temperatures of 2507 and 2521 K, respectively. The congruent melting point of SrZrO3 is 3023 K.
The Zr – C – O system is a promising base for highly refractory oxycarbide ceramics.[209] However, the development of synthetic approaches and identification of the acceptable operating conditions of materials based on the Zr – C – O system at high temperatures are largely complicated by contradictions in the known data on phase equilibria in the system. Vorozhtcov et al.[179] reported the results of simulation of the phase equilibria in the oxycarbide Zr – C – O system using the NUCLEA database and GEMINI2 Gibbs energy minimizer: four polythermal sections and four isothermal sections of the phase diagram were calculated for temperatures 2120, 2500, 3000, and 4097.36 K. As a result, the phases of pure components (two polymorphs of zirconium metal, α-Zr and β-Zr; graphite; and oxygen) were identified in the system, together with the intermediate phases of binary systems such as three zirconium oxide polymorphs (monoclinic, tetragonal, and cubic) and the oxycarbide solid solution ZrCxOy , designated in Fig. 16 and Fig. 17 as FCC_B1.
Fig. 16 shows the calculated section of the phase diagram of the oxycarbide Zr – C – O system at 2120 K.[179] Comparison of the calculated phase equilibria in the Zr – C – O system with experimental data available from the literature [178] showed a satisfactory agreement. Both papers focus on the study of the homogeneity region of the oxycarbide solid solution. The ZrC1 – x-based solid solution was found to dissolve up to 15 mol.% oxygen.
Fig. 17 shows the polythermal Zr – 0.5 C · 0.5 O section of the Zr – C – O system, calculated for the first time up to a temperature of 4100 K using the NUCLEA database, which illustrates the diversity of phase relations in the seemingly rather simple Zr – C – O ternary system.
Thus, the above examples of simulation of high-temperature phase equilibria in oxide and oxycarbide systems using the CALPHAD approach exemplified by the use of the NUCLEA database illustrate the extensive capabilities of this approach. However, the results of the high-temperature description of phase equilibria in the Al2O3 – SiO2 – ZrO2 , La2O3 – SrO – ZrO2 , and Zr – C – O systems attest also to some drawbacks inherent in the use of NUCLEA. These drawbacks can be eliminated only by expansion of experimental studies of the phase diagrams and thermodynamic properties of binary and multicomponent systems, as well as modelling approaches, which allow the most reliable high-temperature description of such systems.
Currently, there are no real options for improvement of the NUCLEA database, which is impossible for a few reasons, e.g., due to restrictions on making corrections, although this could improve the mutual consistency of the data, fill the gaps in the case of appearance of new experimental results, and perform expert evaluation with involvement of newly obtained results.
This circumstance emphasizes once again the need to create a national database of thermodynamic data and models for predicting the phase equilibria in multicomponent oxide, carbide, and oxycarbide systems at high temperatures.
The second part of this Section addresses a number of model approaches that have been widely used in the last decades by our research groups to calculate and predict the thermodynamic properties of multicomponent oxide systems relying on the data for the corresponding binary systems with the assumption that these approaches can be extended to the carbide and oxycarbide systems in order to find high-entropy compounds with specified properties stable at high temperatures.
We will consider both semiempirical methods and the statistical thermodynamic approach, which allowed us to calculate the thermodynamic properties of multicomponent oxide glasses, ceramics, solid solutions, and slag and glass-forming melts at high temperatures.[143, 147-154, 156-158]
The semiempirical Kohler,[210] Toop,[211] Redlich – Kister,[212] and Wilson [213, 214] methods can be used to calculate the excess Gibbs energy in a multicomponent system from the data on the excess Gibbs energy in the corresponding binary systems. These semiempirical methods are based on the assumption that the thermodynamic properties of a multicomponent system are fully determined by the pairwise interactions of the components through the independent contributions of binary systems to an integral thermodynamic property of a multicomponent system while neglecting the influence of ternary and more complex interactions between the components.
The semiempirical geometric Kohler [210, 215] and Toop [211, 215] methods have repeatedly proved to be effective for the calculation of thermodynamic properties in multicomponent systems from the data for the corresponding binary systems in relation to glasses, glass-forming and slag melts, metal,[216, 217] and oxide ceramic [218-222] systems.
The capability of the Kohler method for the calculation of thermodynamic properties of inorganic ternary systems was for the first time demonstrated for glass-forming melts in the Na2O – B2O3 – GeO2 system.[142, 143]
More recent studies devoted to calculations of thermodynamic properties of multicomponent glasses, glass-forming and slag melts, oxide ceramics, solid solutions, and oxide and metal systems by the Kohler method at high temperatures have been surveyed in the literature.[142, 154, 156]
Mention should also be made of a number of later studies that tested the capabilities of the semiempirical methods of calculation of thermodynamic properties of multicomponent oxides using data for the corresponding binary systems for the oxide systems CaO – Al2O3 – SiO2,[218] Na2O – B2O3 – SiO2,[219] Na2O – K2O – SiO2,[219] Gd2O3 – Y2O3 – HfO2,[220] La2O3 – Y2O3 – HfO2,[220] Y2O3 – ZrO2 – HfO2,[221] Sm2O3 – ZrO2 – HfO2,[222] Sm2O3 – Y2O3 – HfO2,[223] TiO2 – Al2O3 – SiO2,[224] La2O – Y2O – ZrO2 – HfO2 ,[225] and Sm2O – Y2O – ZrO2 – HfO2 (Ref. 227) and metal systems Ni – Cu – Co, Ni – Cu – Fe, Fe – Cu – Co, Ni – Co – Fe,[216] and Cu – Ni – Co – Fe.[217]
The Kohler method is symmetric: the binary systems the thermodynamic properties of which are used to calculate the excess Gibbs energy of a multicomponent system are considered to be equivalent. Meanwhile, the Toop method, which is used, unlike the Kohler method, to calculate the thermodynamic properties only of ternary systems, takes binary systems as non-equivalent. For this reason, it is appropriate to use the Toop method when one of the three binary systems markedly differs in physicochemical properties from the other systems.
Semiempirical calculations of the excess Gibbs energy (ΔG ELYZH), e.g., in the La2O3 – Y2O3 – ZrO2 – HfO2 and Sm2O3 – Y2O3 – ZrO2 – HfO2 systems using the corresponding data (ΔG Eij) for the Ln2O3 – Y2O3 , Ln2O3 – ZrO2 , Ln2O3 – HfO2 , Y2O3 – ZrO2 , Y2O3 – HfO2 , and ZrO2 – HfO2 binary systems were reported by Vorozhtcov et al.[225]
Polynomial semiempirical Redlich – Kister [212] and Wilson [213, 214] methods were proposed for solutions of organic compounds and have found wide use in the calculations of phase equilibria in multicomponent systems from the data on the equilibria in the corresponding binary systems.[224] It is noteworthy that these methods for calculating thermodynamic properties of inorganic systems, despite their advantages, have not yet found wide use, especially at high temperatures. The Redlich – Kister and Wilson methods require analytical presentation of experimental data for binary systems based on the corresponding Redlich – Kister and Wilson polynomials and the subsequent extension of the results to a multicomponent system.[226-228]
Stolyarova and Vorozhtcov [228] illustrated in detail the potential of the semiempirical Wilson method for calculation of thermodynamic properties of both binary and ternary systems containing rare earth element oxides from the high-temperature data for the corresponding binary systems. The authors analyzed the validity of calculations of the energy parameters for the interaction of components using the Wilson equation coefficients of binary oxide systems, which they found for the first time at high temperatures. The excess Gibbs energies of the Sm2O3 – Y2O3 – HfO2 , Sm2O3 – ZrO2 – HfO2 (Fig. 18a), and Y2O3 – ZrO2 – HfO2 (Fig. 18b) systems at temperatures above 2000 K were found using the Wilson approach and the data for the corresponding binary systems found previously by high-temperature mass spectrometry,[221, 222, 228] and the results were compared with the Redlich – Kister and Kohler calculation results. The best agreement between the experimental and calculated values for the excess Gibbs energy was found for the Wilson method in the concentration regions far removed from the binary systems.
As follows from Table 3, the ΔGE values obtained by the above semiempirical methods coincide to within not more than 2 kJ mol–1 or 4%. The best fit between the experimental and calculated thermodynamic values was obtained using the Wilson method, with the average deviation of the calculated results from the experimental ones being 9 kJ mol–1 or 31%. Thus, the use of the Wilson method is expedient for estimating ΔGE in the La2O3 – Y2O3 – HfO2 solid solution at xY2O3 < 20 mol.%, where xY2O3 is the mole fraction of yttrium oxide.
A fairly promising approach to the prediction of thermodynamic properties of multicomponent oxide systems at high temperatures is generalized lattice theory of associated solutions (GLTAS),[229] which has been successfully applied in the last 30 years to oxide melts and solid solutions by our research groups.[143, 151, 154]
The first high-temperature application of this approach was to optimize the thermodynamic functions found by high-temperature mass spectrometry for glasses and melts of the B2O3 – SiO2 ,[230] B2O3 – GeO2 and B2O3 – SiO2 ,[231, 232] GeO2 – SiO2 ,[231] B2O3 – GeO2 – SiO2 ,[232] CaO – SiO2 ,[233] and TiO2 – SiO2 – ZrO2 [234] systems.
These studies demonstrated the possibility of thermodynamic description of oxide melts in terms of concentration dependences of the relative numbers of bonds of different types formed in the condensed phase that are calculated taking into account the second coordination sphere. It is also worth noting that the parameters obtained in GLTAS-based calculations were verified by comparing the experimental and calculated viscosities of glasses and melts in the Bi2O3 – B2O3 – SiO2 system.[235]
The GLTAS calculations of the relative numbers of bonds of different types formed in the condensed phase with allowance for the second coordination sphere were verified by comparing the results with the corresponding numbers of bonds determined by IR spectroscopy in B2O3 – SiO2 glasses.[236] In recent years, the results of high-temperature mass-spectrometric determination of the thermodynamic properties of solid solutions of hafnium oxide and rare earth oxide-based ceramics were also supplemented by the results of GLTAS simulation of the Gd2O3 – Y2O3 – HfO2,[237, 238] La2O3 – Y2O3 – HfO2,[220, 238] Sm2O3 – Y2O3, Sm2O3 – HfO2,[226] Sm2O3 – Y2O3 – HfO2,[223, 227] Sm2O3 – ZrO2 – HfO2,[222] Gd2O3 – ZrO2 – HfO2,[239] and Sm2O3 – ZrO2 [240] systems.
The key goal of the modelling of the hafnium oxide and rare earth oxide-based systems was to establish the applicability o a common system of model parameters to binary, ternary, and other multicomponent systems containing common oxide components. For this reason, it was necessary to restrict consideration to the simple lattice model using only three energy parameters for each pair of oxides. It was shown [220, 222, 223, 226, 227, 237-239] that fitting parameters found for identical components in various binary systems are approximately equal to within the experimental error and can be used to calculate thermodynamic properties of other binary systems consisting of the same components. Comparison of the modelling results in series of similar systems [238] usually made it possible to follow the trends of variation of thermodynamic properties, arrange the systems in terms of deviations from the ideality, and draw correlations between the thermodynamic characteristics and the relative numbers of bonds of different types between the selected components of the solid solutions (Table 4).
The dependences shown in Fig. 19a,b unambiguously indicate a correlation of the deviation from the ideality in the La2O3 – Y2O3 , Gd2O3 – Y2O3 , ZrO2 – Y2O3 , and Sm2O3 – Y2O3 systems and the determined relative numbers of mixed type bonds in these systems.
Comparison of the lanthanum oxide activities in the La2O3 – Y2O3 – ZrO2 – HfO2 and Sm2O3 – Y2O3 – ZrO2 – HfO2 systems at 2373 K obtained experimentally and calculated resorting to both semiempirical and statistical thermodynamic approaches (Table 5) attests to correctness of further use of these methods and applicability to a wider range of systems, in particular, for modelling of thermodynamic properties for multicomponent high-entropy systems. Fig. 12 also demonstrates the agreement between the experimental excess Gibbs energy of the melts in the FeO – TiO2 system (which has already been discussed in Section 6.3) at 1760 K and that calculated using the Redlich – Kister polynomial and Wilson polynomial and also the generalized lattice theory of associated solutions.[189]
It should be emphasized that further analysis of the stability of high-entropy oxides and, hence, the prediction of synthesis and application conditions for these materials are difficult without reliable experimental data on the thermodynamic properties of these systems. The results of theoretical calculations of the thermodynamic properties of high-entropy systems should not be considered fully justified and validated without comparison with the experimentally obtained modern values.
Currently, studies aimed at the development and improvement of theoretical approaches to the description of high-temperature equilibria in inorganic systems are underway. For example, Vorozhtcov and Stolyarova [243] reported an original semiempirical approach to calculation of the liquidus temperatures. This semiempirical method makes it possible to estimate the position of eutectic lines in the multicomponent systems using data on the phase equilibria only in binary systems. The applicability of this method for calculating the positions of eutectic lines in the composition – temperature coordinates in multicomponent systems was demonstrated. It was found that the calculated liquidus temperatures for the Gd2O3 – Y2O3 – ZrO2 system (Fig. 20) did not contradict the known data on the phase equilibria in this system to within the relative error not exceeding 3.9%. In addition, the semiempirical method we developed was used to calculate the liquidus temperatures for the Sm2O3 – Gd2O3 – Y2O3 – ZrO2 (Ref. 245) and La2O3 – SrO – TiO2 – ZrO2 – Fe2O3 [244] systems.
It should be emphasized that the proposed semiempirical method for calculation of the liquidus temperatures can in no way replace the results of experimental studies of phase diagrams due to the lack of possibility of predicting the presence of phase separation areas, the occurrence of peritectic reactions, and the formation of compounds.
A benefit of this semiempirical method is simplicity and high speed of obtaining data on liquidus temperatures, which is in high demand when there is no enough time for conducting strict thermodynamic modelling, for example, when it is necessary to predict the possibility of an accident at a nuclear power plant. The proposed method can be used to estimate the position of liquidus curves not only in oxide systems, but also in systems of a different chemical nature. Thus, it is reasonable to additionally test the capabilities of the semiempirical method for calculating liquidus temperatures for metallic, carbide, and oxycarbide systems.
Thus, the use of a wide range of model approaches (semiempirical methods for calculation of thermodynamic properties from the corresponding data for binary systems, statistical thermodynamic approach for optimization of thermodynamic properties, NUCLEA database, semiempirical method for calculation of liquidus temperatures from equilibrium data in binary systems) in combination with experimental studies of vaporization processes and thermodynamic properties is of considerable interest for high-temperature materials science.
8. Conclusion
High-entropy compounds are a promising base for the development of novel materials that are in high demand for domestic science and technology. The unique combination of specified physicochemical properties that can be deliberately obtained and stabilized in high-entropy materials opens up a wide range of applications in electronics, communication techniques, nuclear power engineering, and space and aviation engineering. However, a large portion of the above applications of oxide-, carbide-, and oxycarbide-based high-entropy materials is inextricably connected with the synthesis and operation at high temperatures. This review focuses on this aspect, which is discussed resorting to high-temperature mass spectrometry, one of the most useful experimental methods of high-temperature chemistry to study vaporization processes and thermodynamic properties. The selection of optimal model approaches to predict the thermodynamic properties of high-entropy systems at high temperatures using the equilibrium data for the corresponding binary systems is a highly important condition for evaluation of the thermal stability of high-entropy materials based on oxides, carbides, and oxycarbides. It is noteworthy that the correctness of the model approaches considered in this review has been verified so far only for multicomponent oxide systems. It is possible that the models proposed in this paper will be modified for more successful high-temperature physicochemical characterization of multicomponent carbide and oxycarbide systems as more experimental data become available.
The successful development of modern high-entropy materials stable under extreme high-temperature conditions would be greatly facilitated by the formation of a National Thermodynamic Database for predicting the phase equilibria of multicomponent systems at high temperatures. Presumably, the National Database not only would combine the advantages of the analogous foreign databases, but also would be supplemented by various databases that already exist in Russia for description of the physicochemical properties of inorganic systems, such as the TensorBase database for the thermal expansion of oxygen compounds for various inorganic phases.[245] The further development of high-temperature experimental methods of research into physicochemical properties of high-entropy materials and manufacture of domestic equipment for this purpose would markedly increase the quality of modelling of the physicochemical properties of high-entropy materials in order to check the obtained results, provide original information on the new physicochemical quantities, and enable complete high-temperature description of novel materials with specified properties.[130]
This study was supported by the Grant of the Russian Science Foundation No. 23-13-00254 (https://rscf.ru/en/project/23-13-00254/).
The authors are grateful to A.L.Shilov (Branch of Petersburg Nuclear Physics Institute named after B.P.Konstantinov of National Research Center ‘Kurchatov Institute’ — I.V.Grebenshchikov Institute of Silicate Chemistry) for the invaluable help in preparing and formatting the Figures.
9. List of abbreviations and symbols
CALPHAD — calculation of phase diagrams, an approach to calculation of phase diagrams based on optimization of known phase equilibria and thermodynamic properties,
DFT — density functional theory,
DSC — differential scanning calorimetry,
HEA — high-entropy alloy,
HEC — high-entropy carbides,
HECO — high-entropy oxycarbide,
HEFO — high-entropy fluorite,
HEM — high-entropy material,
HEO — high-entropy oxide,
HEPO — high-entropy perovskite,
REE — rare earth element,
TBC — thermal barrier coatings,
YSZ — yttria-stabilized zirconia.
ai — activity of component i,
ΔSconf — change in the ideal configurational entropy,
ΔH — enthalpy change,
ΔHmix — enthalpy of mixing,
ΔG — change in the Gibbs energy,
ΔGЕ — excess Gibbs energy,
ΔGmix — Gibbs energy of mixing,
ΔS — entropy change,
Δμi — change in the chemical potential of a component,
ΔSЕ — excess entropy,
N — number of components,
R — universal gas constant.
m — sublattice multiplicity,
T — temperature,
xi — mole fraction of component i.
References








































































































































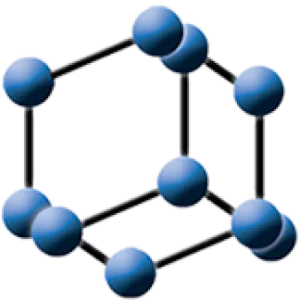































































![Mass loss and corresponding numbers of oxygen atoms per formula unit in the N2/air and H2/air regimes.[26]](/storage/images/resized/TdGyZYio36756YkkVNlQyPQvI1RFtUeNUTnNjj0z_xl.webp)
![Composition of the vapour over the complex carbides Ti2SiC, Ti3SiC2, Ti2AlC, Ti3AlC2, Zr2AlC, and Zr3AlC2 and over the products of carbide interaction with hafnium oxide in the temperature range of 1500 – 2050 K.[161]](/storage/images/resized/5t2rVQUtkyZD8nLUCEJMTz2BFABTn0s23bHkA82Z_xl.webp)
![Component activities (ai) and excess Gibbs energies (ΔGE) in a pyrochlore solid solution in the La2O3 – Y2O3 – HfO2 system at 2337 K, determined using experimental data of high-temperature mass spectrometry (I) and calculated by the Kohler (II), Toop (III), Redlich – Kister (IV), and Wilson (V) methods using the data on equilibria in the corresponding binary systems.[220]](/storage/images/resized/5xMH28fez0TEnI8wXcrY2L0SldRhoYt7OHMM1vDb_xl.webp)
![Parameters of the GLTAS model (bond energies of elements involving the second coordination sphere, kJ mol–1) derived from calculations of thermodynamic properties for binary solid solutions containing lanthanum, samarium, gadolinium, yttrium, zirconium, and hafnium oxides, which were used in the thermodynamic modelling of solid solutions in HfO2-based multicomponent systems at high temperatures.[241, 242]](/storage/images/resized/yYfd3xye8qIsfqwoPrgfSuythwoUJZKQ3yON3eZV_xl.webp)
![Lanthanum oxide activities in the La2O3 – Y2O3 – ZrO2 – HfO2 and Sm2O3 – Y2O3 – ZrO2 – HfO2 systems at 2373 K found experimentally by high-temperature mass spectrometry (I) and calculated by the semiempirical Kohler (II), Redlich – Kister (III), and Wilson (IV) methods and in terms of the GLTAS approach (V).[225]](/storage/images/resized/BMztUq91xtaXWqHvZH4a3VtCMKtqncd2iHH8jzRN_xl.webp)
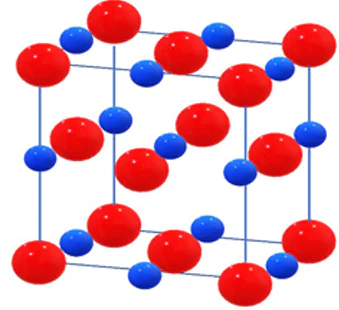
![Configurational entropy as an important condition for stabilization of HEMs. Reproduced from Aamlid et al.[7] with permission from the American Chemical Society.](/storage/images/resized/anfYSVDbOWhMnVS5QwiUwWbRTrculdX0XCTeGKbG_xl.webp)
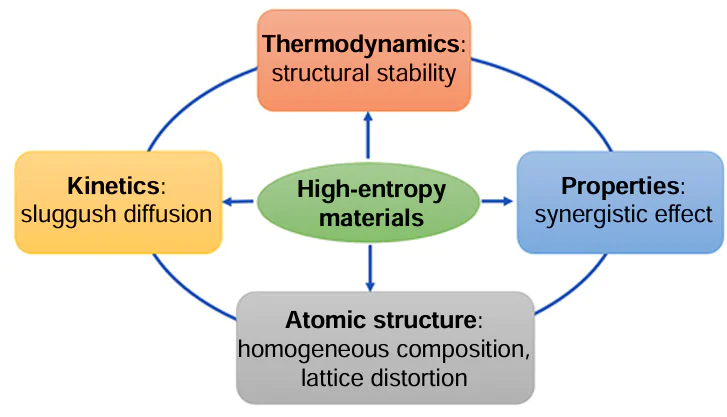
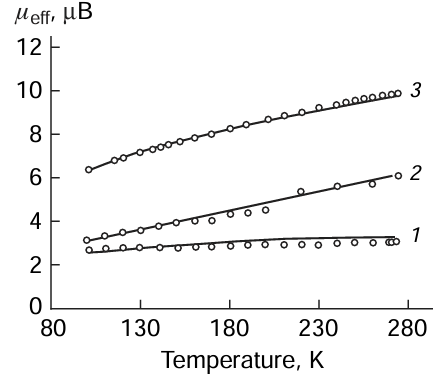
![(a) Crystal structure of the disordered fluorite RE2Hf2O7;[78] (b) thermal conductivities of eight single phase HEFOs and YSZ measured by the time-domain thermoreflectance method:[80] (Hf0.25Zr0.25Ce0.25)(Y0.25)O2–δ (1); (Hf0.25Zr0.25Ce0.25)(Y0.125Yb0.125)O2–δ (2); (Hf0.2Zr0.2Ce0.2) (Y0.2Yb0.2)O2–δ (3); (Hf0.25Zr0.25Ce0.25)(Y0.125Ca0.125)O2–δ (4); (Hf0.25Zr0.25Ce0.25)(Y0.125Gd0.125) O2–δ (5); (Hf0.2Zr0.2Ce0.2)(Y0.2Gd0.2)O2–δ (6); (Hf0.25Zr0.25Ce0.25)(Yb0.125Gd0.125) O2–δ (7); (Hf0.2Zr0.2Ce0.2)(Yb0.2Gd0.2) O2–δ (8). Reproduced from Cong et al.[78] (a) and Gild et al.[80] (b) with permission from Elsevier.](/storage/images/resized/CbLMbfPSH05ClP4YQ8jDIub70klyBG6j9WhNNgo1_xl.webp)
2Zr2O7 (1);(Y0.2Nd0.2Sm0.2Eu0.2Gd0.2)2Zr2O7 (2);(La0.2Y0.2Sm0.2Eu0.2Gd0.2)2Zr2O7 (3);(La0.2Nd0.2Y0.2Eu0.2Gd0.2)2Zr2O7 (4);(La0.2Nd0.2Sm0.2Y0.2Gd0.2)2Zr2O7 (5); and(La0.2Nd0.2Sm0.2Eu0.2Y0.2)2Zr2O7 (6).Reproduced under the Creative Commons CC BY licence.](/storage/images/resized/rFlJCj46Y8VpWI6TJMU7YZjZ9u7pD8TUaTbLzgML_xl.webp)
![(a) Energy of formation (Eform) and (b) enthalpy mixing (ΔHmix) of the following HECs: (TiZrHfV)C4 (1), (TiZrHfNb)C4 (2), (TiZrHfTa)C4 (3), (TiZrVNb)C4 (4), (TiZrVTa)C4 (5), (TiZrNbTa)C4 (6), (TiHfVNb)C4 (7), (TiHfVNb)C4 (8), (TiHfNbTa)C4 (9), (ZrHfVNb)C4 (10), (ZrHfVTa)C4 (11), (ZrHfNbTa)C4 (12), (TiVNbTa)C4 (13), (ZrVNbTa)C4 (14), (HfVNbTa)C4 (15). Reproduced from Liu et al.[96] with permission from Elsevier.](/storage/images/resized/BFFCvYcX7NaCfttnAKKLw4T4G1bbtEaJxW6kibHe_xl.webp)
![Results of testing of the oxidation of high-entropy carbide (Hf0.25Zr0.25Nb0.25Ti0.25)C (HEC) and high-entropy oxycarbide (Hf0.25Zr0.25Nb0.25Ti0.25)(C0.5O0.5) (HECO) samples: (a) change in the sample mass and DSC curves vs. oxidation temperature, (b) change in the Gibbs energy in reactions of the sample oxidation. Reproduced from Wen et al.[18] with permission from Elsevier](/storage/images/resized/SnXagvv0gIi35P4ylDvQgr0Rr22YgFonwpIVfLdd_xl.webp)
![Change in the ideal configurational entropy (ΔSconf) depending on the number of components in equiatomic proportions. Reproduced from Aamlid et al.[7] with permission from the American Chemical Society.](/storage/images/resized/L1uS2BtnF98LsuFWJZUd8eA4XEVAUdzCzQKtzw5P_xl.webp)
![(a) Entropy- stabilized solid solution, (b) enthalpy destabilized solid solution. Reproduced from McCormack and Navrotsky[48] with permission from Elsevier.](/storage/images/resized/h2fyyZKEzJlqfy6wkMtzHY7oKrubkdPLMnAadj4s_xl.webp)
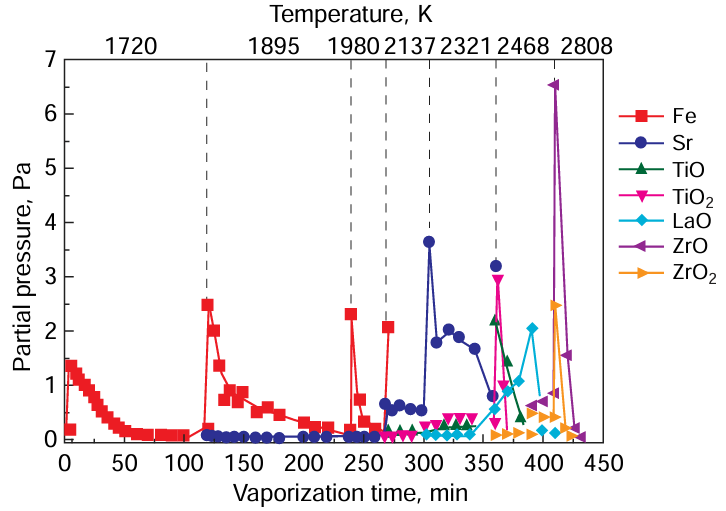
![Excess Gibbs energy (1), (2), and (5), mixing enthalpy (3), and excess entropy multiplied by temperature (4) in the FeO – TiO2 system at 1760 K: (1) calculation using the Redlich – Kister polynomial; (2), (3), and (4) calculation using the Wilson polynomials; (5) result of modelling in the framework of the generalized lattice theory of associated solutions. Reproduced from Stolyarova et al.[130] with permission from Springer Nature.](/storage/images/resized/tf5WIPT0ukDPAPApWuNE6zU2Yzq3lRmkWE6cCkRJ_xl.webp)
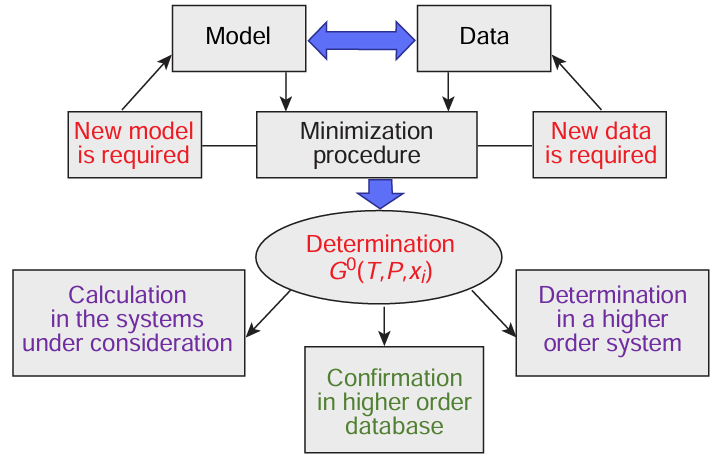
![NUCLEA-calculated isothermal sections of the phase diagram of the Al2O3 – SiO2 – ZrO2 system at 1900 K (a) and 1910 K (b). L is the melt; SiO2 is cristobalite; ZrO2 is the tetragonal phase. Reproduced from Vorozhtcov et al.[203] with permission from Springer Nature.](/storage/images/resized/rv9pJbg17YwyXSyPVeNLgOTGfcROeiGEjaAqSIbo_xl.webp)
![Phase diagram of the SrO – ZrO2 system: (a) experimental data of Gong et al.; (b) calculation results using the NUCLEA data base.[207] Reproduced from Gong et al.[208] (a) with permission from John Wiley and Sons and from Vorozhtcov et al.[207] (b) with permission from Springer Nature.](/storage/images/resized/KixiXDwLe8zNva0f4AWLTQG9uCa06Gy4gzJindip_xl.webp)
![Section of the phase diagram of the oxycarbide Zr – C – O system at 2120 K:[179] FCC_B1 (1), FCC_B1+α-Zr+β-Zr (2), FCC_B1+α-Zr (3), FCC_B1+α-Zr+F-ZrO2–x (4), FCC_B1+F-ZrO2–x (5), FCC_B1+F-ZrO2–x+t-ZrO2 (6), FCC_B1+t-ZrO2 (7), FCC_B1+V (8), C+FCC_B1 (9), α-Zr+F-ZrO2–x (10).](/storage/images/resized/n8KpTXXp7xCCbAL4z1Whsza7OzO91zewtReSdqam_xl.webp)
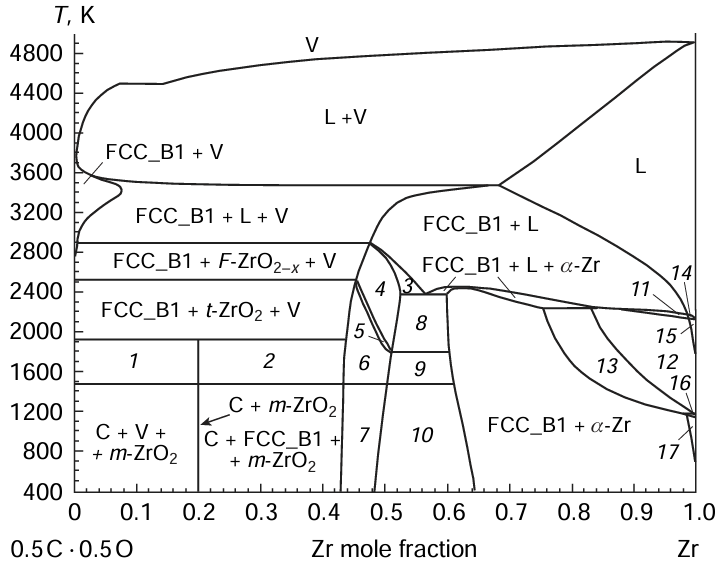
![Excess Gibbs energy: (a) in the Sm2O3 – ZrO2 – HfO2 system at 2373 K and ZrO2 and HfO2 ratio (mole fractions) of 1, (I) ΔGE values found by high-temperature mass spectrometry;[222] (b) in the Y2O3 – ZrO2 – HfO2 system at 2660 K and a constant ZrO2 content of 0.21 mole fraction. (I) ΔGE values found by high-temperature mass spectrometry.223 (II), (III), and (IV) ΔGE values calculated from the data for the corresponding binary systems by the Wilson, Redlich – Kister, and Kohler semiempirical methods, respectively. Reproduced from Stolyarova and Vorozhtcov[228] with permission from Springer Nature.](/storage/images/resized/h3lvMUOu2w25DQxZzJQJryKsz08s6e7pNURPTi3H_xl.webp)
![Experimental excess Gibbs energies for binary systems, La2O3 – Y2O3 (1), Gd2O3 – Y2O3 (2), ZrO2 – Y2O3 (3), and Sm2O3 – Y2O3 (4), determined by high-temperature mass spectrometry and calculated in terms of GLTAS (a) and relative numbers of mixed type bonds calculated with allowance for the second coordination sphere (b). Reproduced from Stolyarova et al.[226] with permission from Elsevier.](/storage/images/resized/KsP6WL3OjAX28wjfNG4TLSRqNfcQLRwdvj611LDQ_xl.webp)
![Liquidus temperatures in the Gd2O3 – Y2O3 – ZrO2 systems at the concentration section with Gd2O3 and Y2O3 mole fraction ratio of 3: solid line is the liquidus temperatures according to [243]; dashed line: (a) liquidus temperatures calculated using the geometric approach; (b) liquidus temperatures calculated using the polynomial approach. Reproduced from Vorozhtcov and Stolyarova[243] with permission from Springer Nature.](/storage/images/resized/5kYuQrJ3WTCTFwnNzEr1kuM6yPcaFqdBzVNwQt9H_xl.webp)