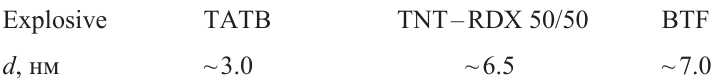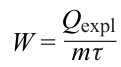Synthesis of nanodiamonds: key patterns and possibilities of control

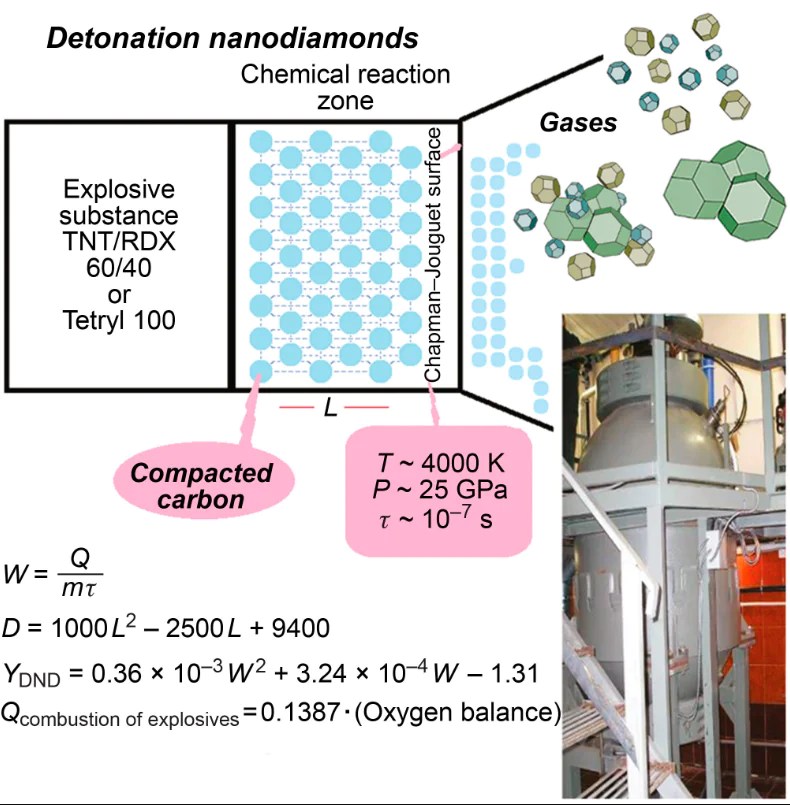
A unique feature of the formation of detonation nanodiamonds (DNDs) is the qualitative incompatibility of highly non-equilibrium conditions (turbulent plasma) in the chemical reaction zone (CRZ) during the detonation decomposition of explosives with the formation of, most often, perfect diamond crystals.

The greatest contribution to investigation of the theory and practice of the detonation synthesis of nanodiamonds was made by V.F.Anisechkin,[1-6] V.V.Danilenko,[7-14] V.Yu.Dolmatov,[15-22] A.P.Ershov,[23-29] N.P.Satonkina,[28] [30-35] V.M.Titov,[12][36-39] A.L.Vereshchagin,[40-46] E.R.Pruuel,[37][38][47-49] V.Pichot,[50][51] J.-C.Arnoult,[52][53] and E.Osawa.[54][55]

The main challenge in the organization of any production that uses DNDs is the invariability of nanodiamond quality. The attempts to elaborate a unified approach to the DND quality have not yet met with success. The quality of DND produced by various manufacturers is often considerably different, being dependent on the particular production and chemical purification processes.

Currently, the most advanced process includes the chemical purification of the detonation diamond-containing carbon (DDC), post-detonation soot, by treatment with dilute nitric acid containing some ammonium nitrate at a temperature of ~ 230°C and a pressure of up to ~ 100 atm.[56] This purification not only provides a low content of incombustible impurities (up to 0.3 mass %), but is also environmentally perfect. In any process using DNDs, their quality is the crucial factor for obtaining a desired product.

Detonation nanodiamonds are characterized by a set of unique properties combining the hardness and inertness of diamond nanoparticles with the high chemical reactivity of the amorphous shell of the nanoparticles. The apparent simplicity of the synthesis makes it possible to produce large quantities of inexpensive nanodiamonds (tens or hundreds tons per year), which is the key conditions for the industrial application of DNDs.

Currently, a ~ 50 : 50 (by mass) alloy or mixture of 2,4,6-trinitrotoluene (TNT) with 1,3,5-trinitro-1,3,5-triazine (RDX) is, in essence, the only charge used to produce DNDs. In some cases, tetryl is used as a single component giving a DND yield of ~ 7.5 mass %.[57]

The synthesis of DNDs is accompanied by the formation of non-diamond carbon species. The detonation product DDC was found to contain carbyne,[8] C₆₀ fullerene,[58][59] onion-like carbon,[60] and carbon oxides.[59]^, [61] DND has a diamond core and a non-diamond shell.[60-65]

The experience in the industrial production of DDC and DNDs under optimal process parameters using a 60 : 40 TNT – RDX mixture in a shell of a 5% aqueous solution of urotropin showed that it is possible to achieve a yield of DDC of up to 13 mass %, a yield of DNDs of up to 8.5 mass %, and a DND content in DDC of up to 72 mass %. The chemical purification of DNDs is performed by nitric acid at a temperature of 230°C and a pressure of up to 100 atm.[56] [63] The use of a charge shell consisting of a 5% aqueous solution of hydrazine or urea leads to a DND yield of ~ 6.0 and 7.0 mass %, respectively, and to a threefold decrease in the content of incombustible impurities in DNDs compared to the standard protocol.

The gas environment formed upon detonation of a blank charge made of the same explosives is traditionally used in the explosion chamber.

The quality of DNDs depends on numerous factors including surface modification of purified nanoparticles. However, what is most important, the use of the same starting material (e.g. 50 : 50 alloy of TNT and RDX) to prepare DDC and for its chemical purification to DNDs by different manufacturers does not give nanodiamonds of a constant quality. Furthermore, currently, there is no technique for the production of DNDs with a content of incombustible impurities below 0.1 mass %, which is a key factor for the use of DNDs in medicine, electronics, surface superfinishing, CVD growth of defect-free diamond films, storage of cold neutrons, etc. In addition, an important challenge is the necessity of preparing stable DND suspensions in inorganic and especially organic solvents with a concentration of more than 0.5 mass % for all applications.

A key issue for the industrial production of DNDs is to normalize their properties irrespective of the production method and mechanism, which may be achieved only by unification of the production conditions. The DND properties depend on numerous factors: explosive type, power, and density; conditions of synthesis, in particular the gas medium in the chamberl the presence of the necessary shell around the charge, etc. An unusual possible solution to the problem of unified quality of DNDs is to commence an initially large-scale DND production plant with a capacity of ~ 1 ton per year by one manufacturer and development of nanodiamond applications based on this production plant.

In the synthesis of DNDs that starts in the turbulence zone of CRZ, crystallization of nanodiamond particles of equal size is impossible. Today, scientists cannot explain the formation of DND particles with a classic cutting over an exceptionally short time of synthesis (0.1 – 0.3 μs).[2][10][62][66-82] The diamond microparticles formed from graphite behind the detonation wave front are composed of plate-like rather than cubic crystals, which is a result of martensitic phase transition of graphite sheets.[83][84]

The diamond and non-diamond carbon components of DDC form a spatially organized structure rather than a chaotic mixture.[85] The results of studies indicate [84] that the non-diamond carbon present in DDC is located along particle boundaries as spatially ordered structures. When DND is completely converted upon heating at Т ~ 1600°C, non-diamond carbon is transformed into nanographite.[86]

The goal of this review is to systematize new empirical and theoretical data concerning the detonation synthesis of nanodiamonds.[53][87-91]

A particular explosive and the structure of its molecule determine the detonation characteristics, and hence the properties of the detonation products (DPs). In the deficiency of oxygen (negative oxygen balance), DPs contain free carbon, which can exist as DNDs and various allotropes of non-diamond carbon.

The selection of explosion conditions is of crucial importance for minimization of the degree of conversion of DNDs to non-diamond carbon. This conversion can take place during expansion of the detonation products. When the temperature drops below 1600 K, the conversion of DNDs to graphite-like structures ceases. However, temperatures promoting graphitization of DNDs appear again in the subsequent stage of the process. During the expansion, the internal energy of DPs is converted into kinetic energy. The retardation of the expansion by the chamber wall leads to the conversion of this energy back into internal energy. This occurs upon extension of explosion waves, which are reflected from the chamber wall, interact with one another, and compress DPs back. Although the pressures are relatively low (2 – 10 GPa), the temperature may exceed the critical graphitization temperature. If the chamber is filled with an inert gas, part of the explosion energy is spent for compression and heating of this gas. This leads to decreasing temperature and helps to preserve DPs.

The transition of the product of synthesis to the gas phase is hampered by the presence of charge shell. The destruction of the shell consumes some of the explosion energy and thus decreases the temperature of DPs and the gas medium. In addition, another function of the shell is to increase the time of expansion of the detonation products. Thus, the role of the shell is to dissipate the energy of the explosion and to increase the time it takes for the pressure and temperature to drop, which helps to preserve and improve the structure of the diamond.

It was shown that upon the detonation synthesis using a TNT – RDX mixture, the main part of DNDs (~ 95 mass %) is formed from carbon contained in TNT.[92]

It was shown[93-96] that the pattern of dependence of the detonation velocity on the charge density for certain explosives changes in the vicinity of 1250 – 1300 kg m^–3 density values. It was noted that no such dependence was present for explosives characterized by positive or nearly zero oxygen balance where DPs contain no free carbon.

When the initial density is moderate, free carbon is condensed in DPs as the graphite phase. When a particular charge density and, hence, a particular pressure in DPs are achieved, carbon starts to be condensed not only as the graphite phase, but also as the diamond phase, with both phases coexisting.

The optimal conditions for the synthesis of the diamond phase of carbon in DPs generated from carbon-rich explosives were found to include high detonation pressure and relatively low detonation temperature. A pressure rise and decrease in the temperature of DPs are facilitated by increase in the initial density of the explosive. Explosives of this type are, for example, 1,3,5-triamino-2,4,6-trinitrobenzene (TATB), hexanitrostilbene, 1,3,7,9-tetranitro-6H-benzotriazolo[2,1-а]benzotriazol-5-ium (Z-TACOT), diaminotrinitrobenzene, and mixtures of carbon-rich explosives with potent high-density explosives such as RDX or HMX.

As DPs pass the Chapman – Jouguet plane,^* they are rapidly expanded and the diamond particles are cooled down to a temperature below graphitization temperature. Initially, the temperature decreases because of the adiabatic expansion of DPs. The expansion velocity depends on the type of explosive, the state of the surface, the charge geometry, and, to a lesser extent, on the atmosphere in the explosion chamber.

The subsequent stage is characterized by intense heat and mass exchange between DPs and the medium surrounding the charge. The main parameters that affect the final temperature and the rate at which it is established are the heat capacity, amount, and chemical reactivity of the medium. Carbon dioxide is the most appropriate gas for cooling at this stage.

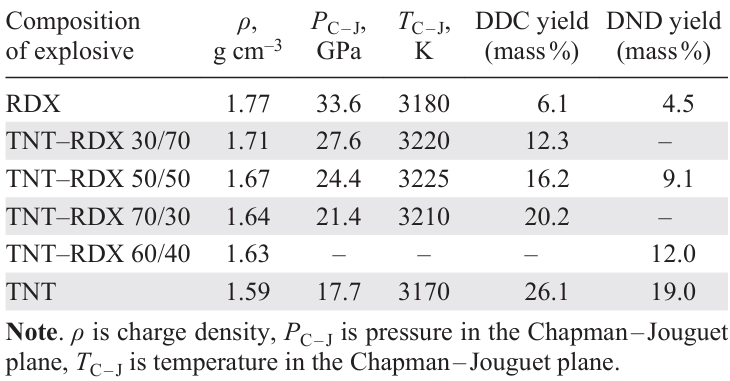
Babushkin et al.[95] reported a theoretical study of the influence of the medium surrounding the charge and the mass of the explosive on the yield of DDC. Initially, pressure P, temperature T, and the chemical composition in the Chapman – Jouguet plane for mixtures of TNT and RDX of various compositions were calculated in terms of the thermodynamic ideal detonation model. The calculations showed that thermophysical and chemical properties of the medium surrounding the charge are the key factors that influence the DDC yield (Table 1). The authors suggested that the interaction of DPs with the medium leads, at a certain stage, to chemically equilibrium state, which finally determines the yield of DDC.

Table 1

\[ \]

Calculated parameters for the synthesis and yield of DNDs.⁹⁵

(1)

More recent experimental data showed that the calculated yields of DNDs and DDC were highly overestimated.[10][14-18][22] [52][62] [93]

A review [96] describes the trend towards increasing yield of DNDs upon increase in the pressure in the Chapman – Jouguet plane from 20 to 25 GPa. Actually, the conclusion drawn in this publication is that selection of explosion conditions should include the selection of the charge mass and size; properties and pressure of the inert gas that occupies the chamber; and the type and size of the charge shell.

Pichot et al.[50][51] investigated the effect of microstructure of explosives, in particular, the size of TNT particles in a mixture with a higher energy explosive on the size of primary nanodiamond particles (6.2 nm particles were formed). When the same compositions of explosives and charge densities were used, nanostructured explosives (TNT particles in a TNT – RDX mixture of ~ 100 nm size) provided the formation of 4.2 nm nanodiamonds.[51] In a later study,[52] nanodiamonds with a particle diameter of 2.8 nm were produced using a nanostructured HMX – TNT mixture with TNT particle size of ~ 40 nm (the nanodiamond synthesis was confirmed by high-resolution transmission electron microscopy (HRTEM) for more than 1000 particles. The authors explained this result by a higher density of nucleation of nanodiamonds in nanostructured explosives.

* The Chapman–Jouguet plane is a plane in which the energy release in CRZ stops and which separates CRZ and the expanded detonation products (Taylor expansion wave).

To date, there is at best a fragmentary understanding of the processes that take place in the chemical reaction zone where precursors of the future diamond nanoparticles are nucleated. The major energy release from thousands of simultaneous chemical reactions takes place in CRZ in which the maximum temperature (3500 – 4300 K) and pressure (20 – 35 GPa) are reached.

The invariability of these parameters provides normal (sustained) course of the detonation process. Since for the formation of DNDs, the oxygen balance (OB^*) of explosives should be in the range from –35 to –55%,[17] carbon previously bound in molecules is inevitably released in the free state, with a part of carbon, as shown by experiments, being released as nanodiamond.[7]

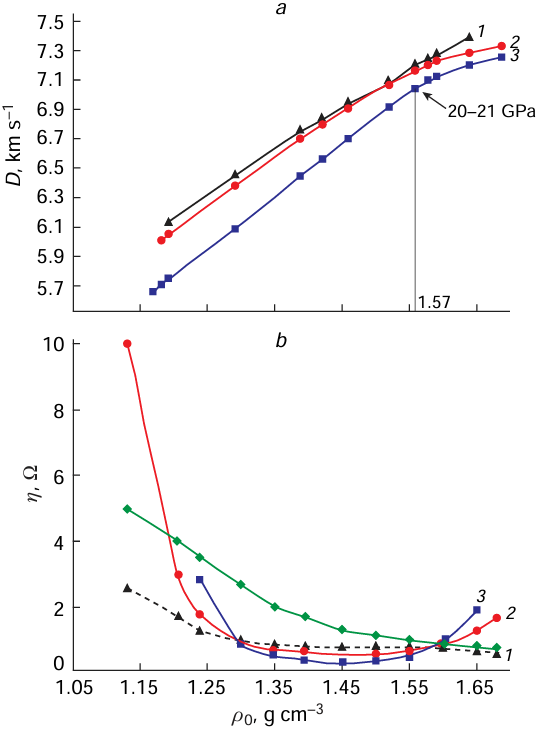
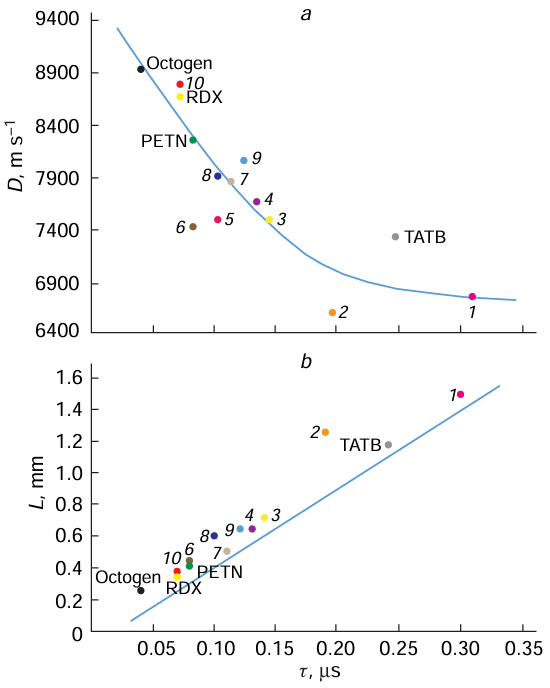
Urizar et al.[97] identified an inflection in the plots for the detonation velocity of TNT – RDX alloy, 2,4,6-trinitrophenyl-N-methylnitroamine (tetryl), and 2,4,6-trinitrophenol (picric acid, PA) vs. charge density (Fig. 1a). Later, it was suggested[98][99] that this inflection is, most likely, caused by the onset of DND formation.

Fig. 1

Dependences of the (a) detonation velocity D on the initial charge density ρ₀: (1) TH 50/50, (2) tetryl, and (3) 2,4,6-trinitrophe nol; and (b) electrical resistance of DPs (η) on the charge density: (1) 2,4,6-trinitrophenol, (2) tetryl, (3) RDX, and (4) TNT – RDX 50/50.⁹⁷

More recently, Antipenko et al.[100] detected the second inflections in the same dependence for the detonation of TNT – RDX charges (3/1 and 1/1); in this case, it was assumed that the DND formation has been completed. A study of the same detonation process by electrical conductivity measurements showed a significant drop in the conductivity (i.e., an increase in the electrical resistance). This finding was interpreted [101] (Fig. 1b) by assuming the formation of nanodiamond the electrical conductivity of which is negligible compared to that of non-diamond carbon. However, according to the modern views, the proper DND cannot be formed in CRZ. The Р,Т conditions in CRZ rule out the possibility of carbon crystallization. In addition, there is no possibility for heat removal. Non-conductive dense plasma-like carbon structures, which are in essence precursors of nanodiamonds, can be formed in the reaction zone. These structures crystallize or amorphize only beyond the C – J plane where heat removal is possible.

The first inflection (Fig. 1a) in the D( ρ₀) curve for tetryl corresponds to a C – J pressure of 20 – 21 GPa (Ref. 102) and a charge density of 1.58 g cm^–3. Comparison of the two plots (a) and (b) indicates that the author’s statement that the minimum electrical conductivity of DPs and the first inflection in the D(ρ₀) curve coincide in the charge density is not true. Indeed, the inflection point for, e.g., tetryl corresponds to a density of 1.58 g cm^–3, while the minimum electrical conductivity corresponds to 1.48 g cm^–3. This difference is significant, which attests to the difficulty and ambiguity of DND synthesis. Nevertheless, the cited study [102] was continued by Aleshaev et al.,[103] who proved that the nucleation of the nanodiamond pre-structure actually starts in CRZ, while the formation of proper DNDs is possible only when DPs (both gaseous and condensed products) migrate beyond the C – J plane where heat removal from the condensed carbon is possible.

The self-sustained detonation is maintained if the velocity of plasma-like matter in CRZ corresponds to the detonation wave velocity (6 – 8 km s^–1); however, the mass velocity of gaseous products beyond the C – J plane is much lower for both single-component and mixed explosives, being ~ 2 km s^–1.[102] The matter that flows inside CRZ is a ‘plasma’ (Т ~ 3000 – 4500 K and Р ~ 20 – 35 GPa). After cooling, DPs mainly consist of N₂ , H₂O, C, CO, CO₂, NO, NO₂, CH₄, O₂, N₂O, and HCN. In the case of detonation of powerful condensed explosives, the density of DPs in CRZ is 2.2 – 2.5 g cm^–3, which is markedly higher than the density of the starting explosives (~ 1.6 – 1.7 g cm^–3). The release of energy from the degradation of explosive molecules continues beyond the C – J plane (~ 15% of the total explosion energy).[10][62]

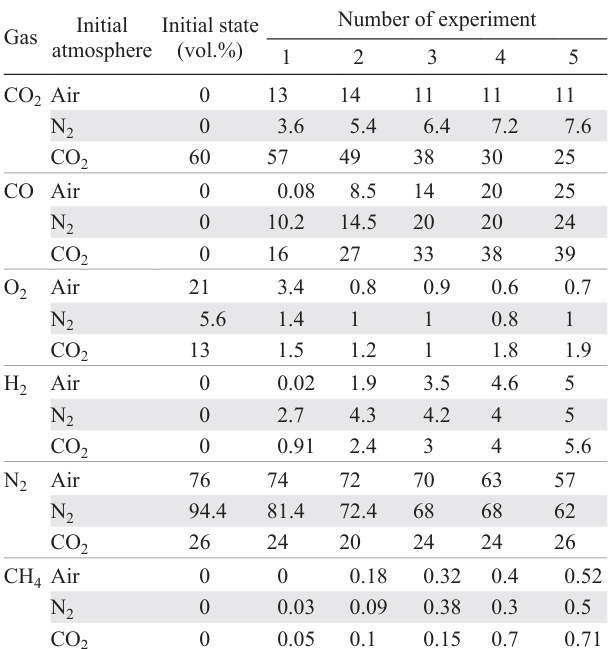
There is only one published study[104] in which the gas composition after the explosion in the DND synthesis was determined, in particular, the authors experimentally analyzed the gas phase of the detonation products after explosion of TNT – RDX 40/60 in atmospheres of air, N₂ , and CO₂ . Five detonations were carried out in each initial atmosphere in a ~ 2 m³ Alpha-2M explosion chamber. The charges were exploded successively one after another. After each explosion, the gas in the chamber was analyzed. The mass of each charge was ~ 650 g, and the density was ~ 1.62 g cm^–3. The charge was detonated using a standard method. The accuracy of the analysis was no less than 1.5%.

The data on the changes in the gas composition (before and after detonations of identical charges) are summarized in Table 2. In all experiments, the product of incomplete oxidation of carbon appeared immediately in each gas atmosphere, with the amount of carbon monoxide being considerable and increasing with increasing experiment number. It should be noted that CO was absent in the calculations due to the lack of stability and appeared only upon isentropic expansion of DPs to specific volumes of 0.1 m³ kg^–1. As follows from Table 2, the content of oxygen is moderate in all cases after the first detonation.

Table 2

\[ \]

Gas phase composition in the explosion chamber after each of the five detonations of TNT – RDX 40/60 for different initial gas atmospheres.¹⁰⁴

(2)

The contents of combustible gases such as hydrogen and methane increases with increasing experiment number, with the hydrogen content reaching 5.6 vol.%. The nitrogen content decreases with each experiment, being however still relatively high. Carbon dioxide appears in a considerable amount immediately after the first detonation of the charge, while the subsequent increase in the CO₂ concentration is insignificant. A 40 – 60 vol.% content of carbon dioxide can be achieved by purging the chamber with CO₂ . For the subsequent experiments, the amount of CO₂ decreases, but still remains relatively high.

Upon expansion, the gaseous DPs hit the wall of the explosion chamber, their thermal energy is converted to the kinetic energy, and DPs move towards each other, while passing through the central part of the chamber.[24] This takes place many times, and so-called ‘hot nucleus’ is formed at the centre of the chamber. The temperature is markedly above 1600°C, i.e., it exceeds the temperature of diamond graphitization, but the pressure is low. Thus, the yield of DNDs decreases due to partial graphitization. However, the hot nucleus does not appear in the carbon dioxide atmosphere due to its high heat capacity; therefore, the yield of DNDs is much higher when CO₂ is used.

When air serves as the gas medium, the high concentration of oxygen in air (~ 21 vol.%) precludes the possibility of preserving the DNDs that formed. As the number of detonations increases (see Table 2), the concentration of CO₂ reaches a maximum after the first detonation, then decreases as a result of partial dissociation, and reaches a constant value (11 vol.%) as soon as after the third detonation of the charge. However, the amount of carbon monoxide, conversely, considerably increases to reach a maximum of 25 vol.% by the fifth detonation. This effect is related not only to the dissociation of CO₂, but rather to oxidation of solid carbon (DDC).

The high concentration of carbon in the molecules of the starting explosives (23 – 34 mass %) and the negative oxygen balance (–35 to –60%) account for high concentration of carbon in CRZ. The existing Р,Т-conditions and high concentration of carbon caused by negative OB generate conditions for the consolidation of carbon into dense structures, which are DND precursors;¹⁹ meanwhile, destruction of the formed carbon structures hardly takes place.

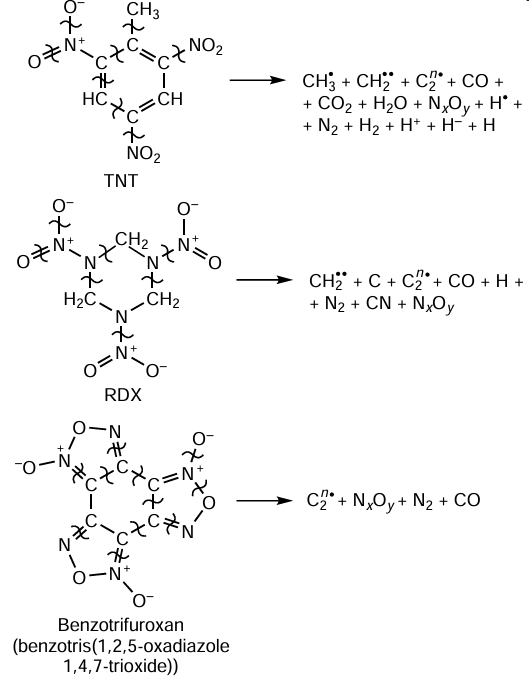
The earlier point of view [12][103-109] according to which the molecules of the starting explosives decompose into atoms in the detonation wave is untenable, because there is no sufficient energy for this process.[19][62] Indeed, cleavage of all bonds between atoms in the molecules of hydrogen-containing TNT and RDX and hydrogen-free benzotris(1,2,5-oxadiazole 1,4,7-trioxide) (benzotrifuroxan, BTF) requires 4 – 5 times more energy than it is released upon explosion. Therefore, the bottom-up assembly of nanodiamonds from the atomic level [12][105][106][108][109] is unrealistic. In addition, during cooling of liquid carbon (after the C – J plane has been passed), crystallization begins at the surface of the nanodroplets (cooling surface), and in view of the virtually perfect structure of the inner core, which is diamond in the cubic crystal system, and disordered structure of the outer shell of DND nanoparticles, this process can hardly be conceived.

The decomposition of explosive molecules corresponding to three classes of organic compounds is depicted in Scheme 1.[19]

Scheme 1

The detonation of each of these explosives gives DNDs. However, the yield of nanodiamonds is low: 0.8 – 1.0 mass % from TNT or RDX or ~ 1.8 mass % from BTF. Nevertheless, it is clear that there must be a common precursor to the formation of future DND crystals;[16][19] most likely, this is the C₂^n• polyradical.

The form of existence of DND precursor in CRZ is still a debated issue. Due to the absence of heat removal from the carbon nanoparticles formed in CRZ and to the high pressure and temperature, crystallization of nanodiamond is impossible. Most likely, the ‘excess’ carbon as the only non-gaseous product is self-organized to a condensed phase, as was actually shown.[103][110] It can be assumed that, despite the chaos and high turbulence of matter in CRZ, a certain order maintained by extremely high pressure (20 – 36 GPa) is still present (otherwise, a stable detonation process would be impossible). Hence, there is a probability of formation of a 3D fractal network.[19] At the nodes of this network characterized by a higher density, there is enough time for condensed carbon to form a sort of ordered 3D core, while the sites characterized by a lower carbon density break and recombine many times during DP expansion. Thus, the DND pre-structure is either a dense plasma-like carbon core, which becomes liquid carbon beyond the C – J plane, or the formed energetically favourable cyclohexane carbon skeleton. The interaction of these structures with one another beyond the C – J plane is accompanied by further decrease in energy and by rearrangement to give adamantane type radicals, which are attacked by the C₂^n• radicals (diffusion mechanism of nanodiamond formation). Perhaps, both mechanisms of DND formation operate simultaneously. This is followed by crystallization (amorphization) of liquid carbon or cooling down of DND crystallites formed by the diffusion mechanism from the adamantane pre-structure.[16]

It was shown [92] [111][112] that when TNT labelled with ¹³C in the methyl group[111] or with ¹⁴C at position 1 of the benzene ring [92][112]is used as a mixture with RDX or HMX, respectively (this is not important), the future DND particles are mainly formed from the TNT carbon atoms (up to 93%). The authors attributed this result to two possible causes: separate degradation of each explosive particle: TNT, RDX, and HMX (the particle size in a mixture can range from a few to hundreds of micrometres), because DPs of these compounds have no time to move during the chemical reaction (0.1 – 0.3 ms) or different rates of formation of diamond-like particles from different fragments of TNT, RDX, and HMX decomposition. The markedly lower degree of conversion of RDX carbon into diamond can be attributed to considerably higher (–21.6%) oxygen balance compared to that of TNT (–74%) and the lower release of condensed carbon. The kinetic limitations are due to the fact that RDX molecule can produce only single carbon atoms upon decomposition, while TNT can degrade into fragments containing a few carbon atoms bound to each other.

Since detonation of TNT provides a very low yield of DND (~ 1 mass %) and the addition of powerful RDX, which separately also gives a low amount of nanodiamond (~ 1 mass %), results in a yield of up to 8.5 mass %, not only OB, but particularly the methyl radical in TNT may play a role.[19] In other words, it is possible that both C₂^n• and CH₃^• competitively participate in the formation of nanodiamond pre-structure. It was shown[113] that replacement of TNT in a mixture with RDX by trinitrobenzene, with all other factors being the same, leads to an almost 1.5-fold decrease in the nanodiamond yield: from ~ 8.5 to ~ 5.5 mass %. Thus, the methyl radical of TNT is very important for increasing the yield of DND.

For crystallization of nanodroplets upon the isentropic expansion of DPs, the nanodroplets should be cooled down by colder molecules of the expanding gaseous DPs. Apart from the temperature difference, cooling requires intense flow of DP gas molecules around the nanodroplets. In DPs, this flow around the nanodroplets is provided by microturbulence and separation.[114] The microturbulence arises in CRZ and is caused by non-uniformity of the explosive (heterogeneity, porosity, anisotropy), while separation also originates in CRZ, but develops during the isentropic expansion of DPs. The separation phenomenon implies the separation of an initially homogeneous mixture of particles of different weights in a flow. In DPs, this is a series composed of nitrogen, water, carbon oxides, and carbon nanoparticles. Detonation products start to move beyond the C – J plane at a mass velocity of approximately 2 km s^–1 along the axis of the charge, and during movement, the much heavier carbon nanoparticles gradually start to lag behind, and thus the concentration of nanoparticles at the tail of the flow increases, and so does the probability of collisions and coalescence. The lag increases with increasing weight of nanoparticles and with increasing time of movement and decreases with decreasing flow velocity.

The termination of growth of nanodiamond particles is, most likely, due to the following two factors:[61] the emergence and accumulation of growth defects, that is, the occupancy of the coordination spheres by carbon atoms may occasionally decrease (the bond length increases) or increase compared to the number of carbon atoms in the perfect diamond structure; and decrease in the number of carbon radicals because of their consumption and recombination. As a rule, DNDs have bi- and trimodal size distribution in the range from ~ 2 to ~ 11 nm depending on the conditions of synthesis. The shell around the diamond core is 3.91 Å thick and has a structure that does not correspond to the diamond structure outside the coordination sphere the radius of which (R_CS) varies from R_CS = 38.48 Å to R_CS = 43.19 Å.

The change in the size of the arising carbon particles after they pass the detonation front was studied by small-angle X-ray scattering (SAXS).[37] [103][110] Immediately after the front, a carbon nanoparticle measuring 1.0 – 1.5 nm is detected. Then the particle grows to reach a size of 2.5 – 3.0 (TATB), 6 – 7.2 (TNT – RDX 50/50), and ~ 7.0 nm (BTF) over a period of 3 – 4 ms (Table 3).

Table 3

\[ \]

DND particle size depending on the type of explosive.¹¹⁰

(3)

It should be noted that small-angle X-ray scattering is suitable only for determining the size of carbon particles, while determination of the type of their structure (graphite or diamond) requires the use of other methods.

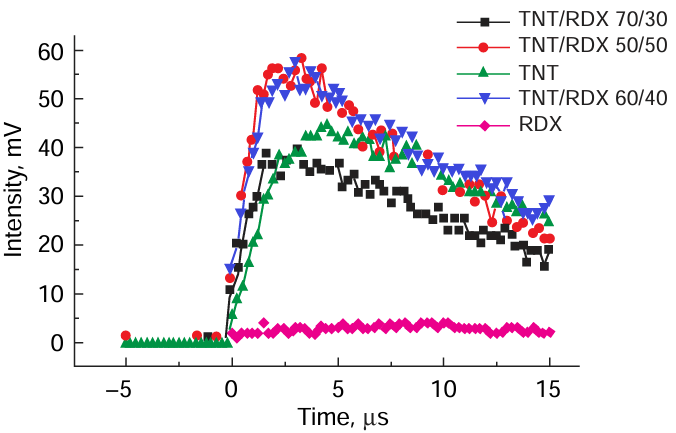
In order to be investigated by SAXS, condensed carbon should have a density exceeding 2.5 g cm^–3, i.e., it should be above the density of ‘plasma’ in CRZ. The SAXS signal detects condensed carbon even in the chemical reaction zone (CRZ) for TNT, RDX, and TNT – RDX mixtures (70/30; 50/50; 60/40). It was found [37][103] [110] (Fig. 2) that the condensed phase of carbon, which has an increased density, appears immediately after the detonation front has been passed for TNT and TNT – RDX charges. The fast increase in the SAXS signal lasts for up to 1.8 ms. This is followed by a sort of plateau (up to 4.4 ms) and then by a slow decline up to 15 ms and after that.

Fig. 2

SAXS characteristics of nucleation and growth of particles of the condensed carbon phase in CRZ during the expansition of DPs of condensed carbon-containing explosives

The formation of DND pre-structure obviously starts in CRZ, but a tightly bound diamond–non-diamond carbon structure (DDC) is arranged far beyond CRZ. According to calculations, the matter travels a distance of 4.4 mm in 1.8 ms (this distance is ~ 35% of the charge diameter, which is ~ 12 mm) and a distance of approximately 9.5 mm (77% of the charge diameter) in 4.4 ms. In essence, this is the zone of formation of DNDs in the form that we already know; the formation of DND crystallites is completed in the range from 1/3 to 3/4 of the charge diameter (4.4 – 9.5 mm). This is followed by sharp pressure and temperature drops accompanied by the attack of the newly formed nanocarbon, including DND crystallites, by corrosive gases (CO₂ and H₂O), which leads not only to a decrease in DDC crystallites, but also to graphitization of DND crystallites.

Thus, immediately after passing the detonation front, primary carbon plasmoids that can be detected by SAXS are formed within 10^–8 to 10^–9 s. As a plateau is reached, i.e., at a distance of 1/3 – 3/4 of the charge diameter, a complex DDC structure with a DND crystallite as an inner core and amorphous carbon particles as the outer shell is ultimately formed. The high yield of DNDs is achieved when 28 – 35 mass % of the total amount of carbon present in the mixed explosive molecule is spent for the formation of free carbon.[115][116] A CRZ with a size of ~ 0.6 mm, which is a rather long distance, is needed for the formation of DNDs in a high yield (≥ 5 mass %). This provides the following conclusion: the time of existence of the relative plateau for TNT – RDX charges is 1.8 to 4.4 μs, which corresponds to a 4.4 – 9.5 mm distance (1/3 – 3/4 of the charge diameter) from the detonation wave front.

Dolmatov et al.[116] concluded that the density of the plasma-like carbon in CRZ may vary from 2.6 to 3.3 g cm^–3, and the plasmoids may exist as nodes of a carbon fractal network.

* Oxygen balance is the ratio, expressed as a percentage, of the sum of weights of oxygen and hydrogen remaining after the oxidation of all carbon contained in the explosive molecule to carbon dioxide and all hydrogen to water to the weight of the original explosive. It is assumed that nitrogen remains in a free state.

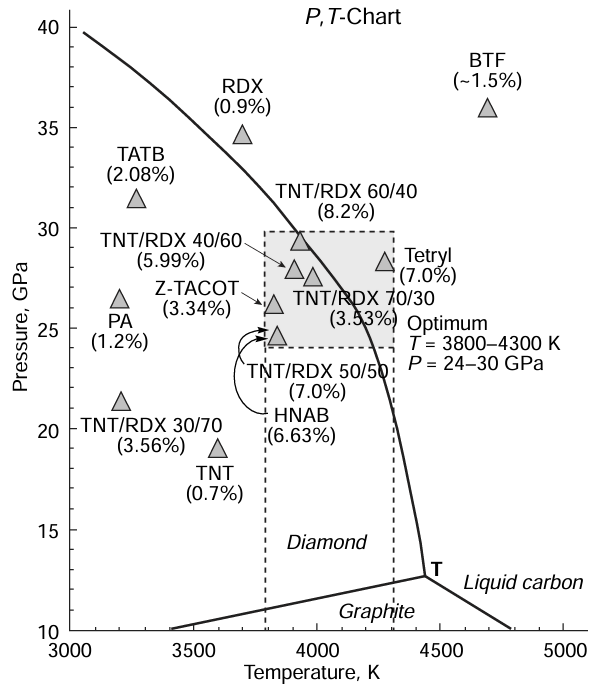
Considering the classic P,T-chart of carbon (Fig. 3), free carbon from TNT (Р ~ 18 GPa, T ~ 3600 K, DND yield of ~ 1 mass %) is not obviously in the liquid carbon state, whereas free carbon from BTF (Р ~ 36 GPa, T ~ 4500 K, DND yield of ~ 1.8 mass %), conversely, falls in the liquid carbon region.[115]

Fig. 3

Dependence of DND yield on the Р,Т-conditions in the phase diagram of carbon.¹¹⁵ T is the triple point at P = 13 GPa, T = 4470 K. HNAB is hexanitroazobenzene

The new data [115] on the DND yield, pressure and temperature in the C – J plane, and composition of explosive charges placed on the phase diagram of carbon, taking account of the oxygen balance and the optimal density, showed that the region of the highest DND yield is confined by a pressure in the C – J plane of 23 – 29 GPa and a temperature in the C – J plane of 3850 – 4350 K; the yield of DNDs in this region is usually 6.1 to 8.2 mass %.

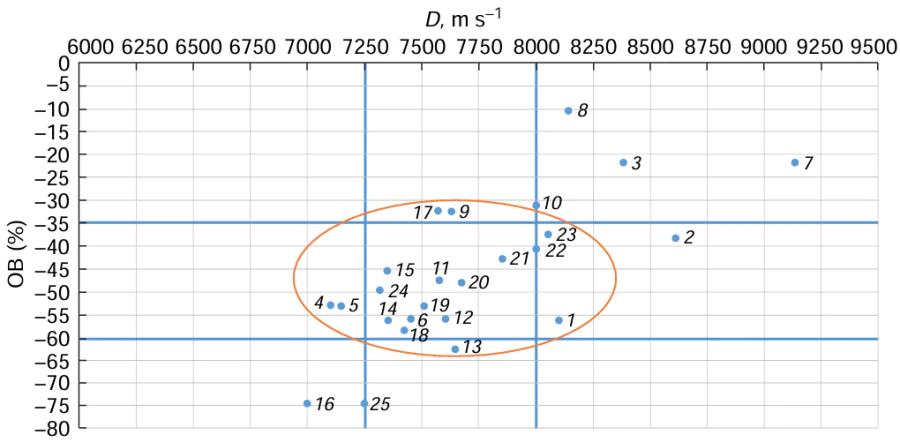
In the first stage of development of new procedures for DND synthesis based on the search for a new sort of raw material (explosive), it is reasonable to use simple methods of probabilistic assessment. The need to search for new sorts of explosives is related to the sharp increase in the cost of TNT, RDX, and tetryl[57] and to the danger of handling explosives in principle. Zhukova[117] listed most types of explosives, some of which can be investigated as possible raw materials. Oxygen balance is a characteristic of explosives that can be easily determined; furthermore, it was shown[17] that the optimal OB of nitroaromatic compounds for the preparation of nanodiamonds is –40 to –55%. The detonation velocity is, most often, the first characteristic to be determined for explosives, and this value can be taken from a reference book (e.g., Ref. 117). Dolmatov et al.[54] elucidated the dependence of the yield of nanodiamonds upon the explosion of nitroaromatic compounds on the detonation velocity. In order to provide a DND yield of at least 5 mass %, the detonation velocity should be in the range of ~ 7.3 – 8.0 km s^–1. Fig. 4 shows the region confined by the 7.3 – 8.0 km s^–1 range along the abscissa and the –35 to –60% range along the ordinate. The explosives that fall in this region can be considered as possible candidates for replacing TNT – RDX alloys and tetryl. These compounds include hexanitrodiphenylamine (HND), hexanitrodiphenyl, tetranitroaniline, tetranitrobenzenes, trinitroaniline, trinitroanisole, 1,3-diamine-2,4,6-trinitrobenzene, trinitro­benzene, and their mixtures.

Fig. 4

Optimal relationship between the detonation velocity (D) and oxygen balance (OB) of explosives to achieve a DND yield of ≥ 5 mass %: (1) aminotrinitrobenzene (trinitroaniline), (2) BTF, (3) RDX, (4) hexanitrobiphenyl, (5) HND, (6) 1,3-diamino-2,4,6-trinitrobenzene, (7) HMX, (8) PETN, (9) tetranitroaniline, (10) tetra nitrobenzene, (11) tetryl, (12) TATB, (13) trinitroanisole, (14) trinitrobenzene, (15) picric acid, (16) TNT, (17) ethylenedinitramine, (18) TNT – RDX 70/30, (19) TNT – RDX 60/40, (20) TNT – RDX 50/50, (21) TNT – RDX 40/60, (22) TNT – RDX 36/64 (pressed), (23) TNT – RDX 30/70, (24) HNAB, (25) Z-TACOT.²²

Despite the existence of ‘plasma’, conditions that are necessary and sufficient for the coagulation of excess carbon nanodroplets or the growth of carbon particles by diffusion mechanism are generated in CRZ owing to high pressure and temperature. While passing the C – J plane, the droplets are enlarged during movement and due to collisions and, depending on the heat removal efficiency, they crystallize as either DND particles or non-diamond carbon. It was shown[118] that the contents of elements in the explosive molecule or an averaged molecular formula can be efficiently and easily used for preliminary assessment of the yield of nanodiamonds.

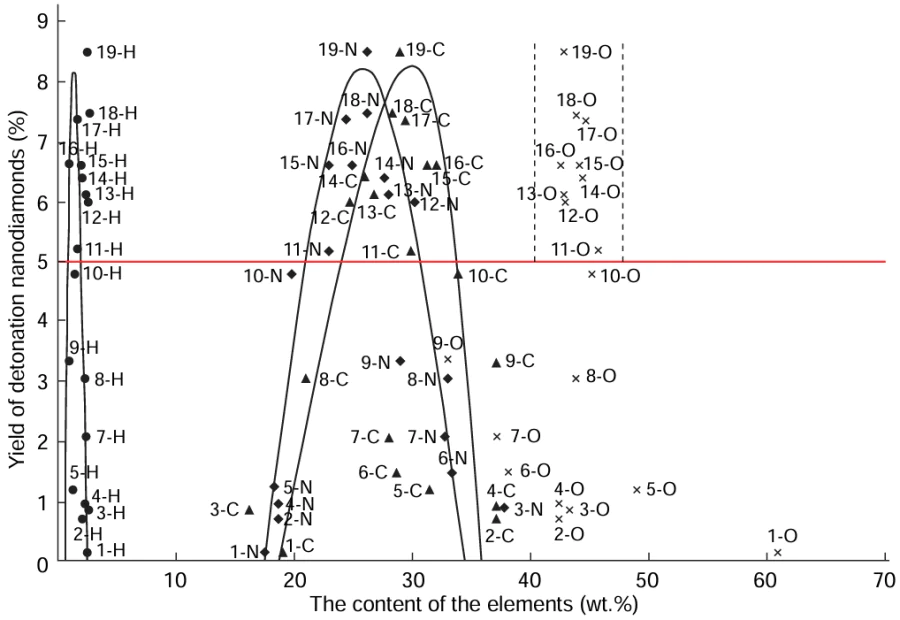
Fig. 5 shows the dependence of the yield of nanodiamonds on the contents of all elements in the explosive molecule. It can be clearly seen that the condition of industrial scalability, that is, a yield of DND of at least 5 mass %, is achieved when the carbon content of the molecule is between 23 and 34 mass %, the hydrogen content is from 1.5 to 3.0 mass %, and the amount of oxygen needed to ensure the detonation of the required intensity is in the range of 42 – 46 mass %. Nitrogen is important, most likely, as a carrier for the oxidizing element, that is, oxygen. The optimal amount is nitrogen is between 23 and 31 mass %. Thus, when these conditions are met (see Fig. 5), all other factors being the same, the DND synthesis in a yield of at least 5 mass % can be expected for powerful carbon-containing explosives.

Fig. 5

Dependence of the yield of nanodiamonds on the elemental composition of explosives.¹¹⁸ The numbers correspond to the contents of elements in the starting explosive.

To date, the synthesis of DNDs from charges composed of TNT and RDX mixtures has been studied fairly comprehensively, and the following optimal values for the major control parameters of the synthesis have been found empirically:

— composition of the charge (~ 60% TNT and ~ 40% RDX),

— charge density (1.6 – 1.7 g cm^–3),[17]

— optimal oxygen balance (–35 to –60),[17]

— presence of a water or water–salt shell around the charge,[119]

— non-oxidizing or, better, reducing atmosphere for detonation.[120]

— the pressure in CRZ should exceed 17 GPa, while the temperature should not be lower than 3000 K.

In the opinion of Dolmatov et al.,[19] [22] determination of the explosive power and related yield of DNDs, all other factors being the same, would provide the most versatile characterization of explosives. The TNT equivalent commonly accepted to define the power of an explosive is a rough characteristic related to the performance of explosive detonation products (strength and brisance) and is not suited as a scientific definition.

The power of a charge, defined in explosion engineering as heat released per unit mass, also cannot be used for accurate calculations and is not suited as a classic definition of power, which is understood as energy release per unit time. Since it is impossible to determine the remaining heat that is released during the DP expansion beyond the C – J plane, it was postulated that all the thermal energy of the explosion is released in CRZ. Currently, it is possible to determine quite accurately both the length and lifetime of the chemical reaction zone. Thus, it became possible to determine the specific power (W) in the classic way, that is, as the ratio of the heat of explosion to unit weight (kg) and unit time (μs).

(1)

where W is the specific power of an explosive, kJ kg^–1 μs^–1; Q_expl is the heat of explosion,^* kJ kg^–1, m is the mass of the explosive, kg; τ is the time of energy release (lifetime of CRZ), μs.

The yields of DNDs were predicted for explosives listed in Table 4.[12][14][107][109][121-125] These explosives may be of certain interest as possible substitutes for TNT – RDX alloys due to the scarcity and high cost of RDX.[109][117] [121][123][126][127] Meanwhile, the yield of DNDs considerably depends on the conditions of detonation synthesis. Al data on DND yields summarized in Table 4 were determined by Dolmatov et al.,[22] with all detonations being conducted in a 2.14 m³ Alpha-2-М explosion chamber, the charges being fabricated and ignited by one and the same operator, and detonation being performed in a water shell.[22]

Table 4

\[ \]

Characteristics of the detonation process of TNT – RDX and tetryl charges.^{12, 14, 107, 109, 121 – 125}

(4)

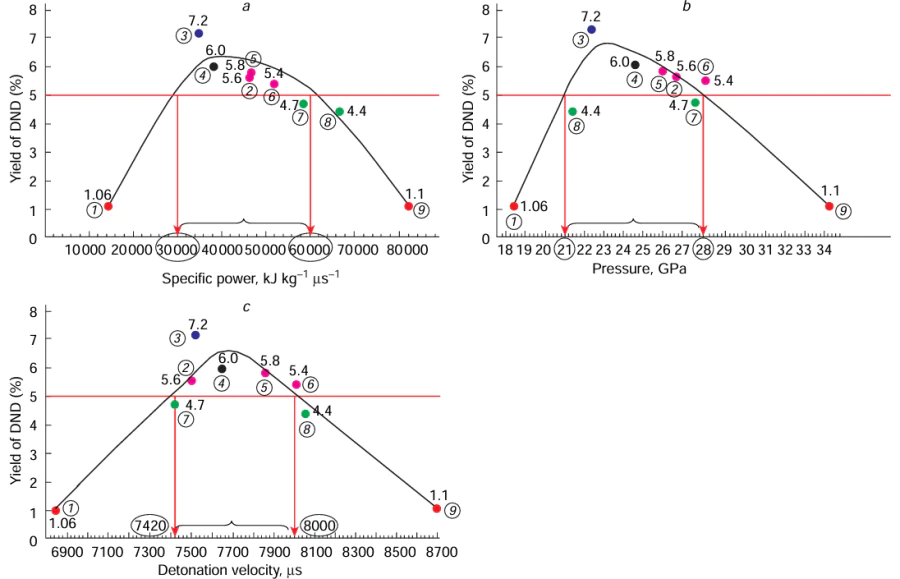
Dolmatov et al.[19] investigated the dependence of the experimental DND yield on the specific power of the explosive, pressure in the C – J plane, and the explosive detonation velocity. The dome-shaped dependence of nanodiamond yield on the explosive specific power indicates (Fig. 6a) that both too low and too high power considerably decreases the yield. The optimal power of the explosive is in the range from 30 to 60 kJ kg^–1 μs^–1. This condition is met for the TNT – RDX 60/40 alloy. Satisfactory yields can be achieved for TNT – RDX 50/50, TNT – RDX 40/60, and tetryl.

Fig. 6

Dependences on the DND yield on the power of the explosive (a), pressure in the Chapman–Jouguet plane (b), and explosive detonation velocity (c). (1) TNT, (2) tetryl, (3) TNT – RDX 60/40, (4) TNT – RDX 50/50, (5) TNT – RDX 40/60, (6) TNT – RDX 36/64, (7) TNT – RDX 70/30, (8) TNT – RDX 30/70, (9) RDX.¹⁹

The use of a simpler relationship, the dependence of DND yield on the DP pressure in the Chapman–Jouguet plane (Fig. 6b), indicates that the DP pressure should be between 21 and 28 GPa.

The dependence of the DND yield on the detonation velocity (Fig. 6c) shows that it is necessary to use explosives with a detonation velocity of 7250 to 8000 m s^–1, i.e., if the detonation velocity and the composition of the mixture of explosives are known, it is possible to estimate the yield of DNDs from this explosive mixture with sufficient accuracy.

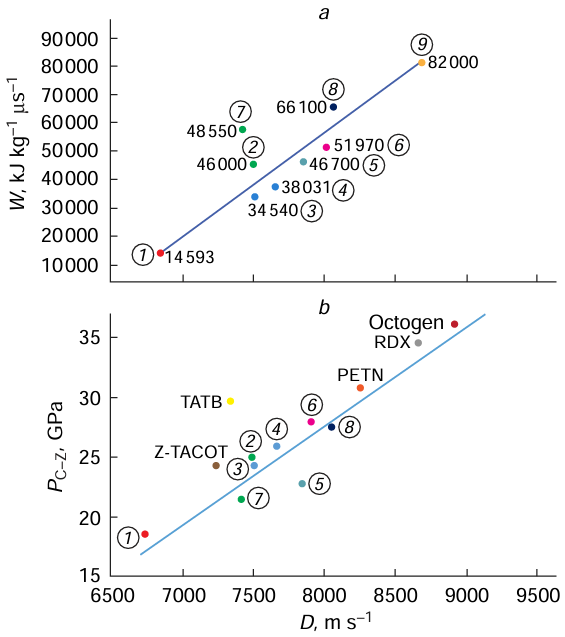
Fig. 7a presents the virtually directly proportional relationship between the detonation velocity and the power of explosives. Thus, from known detonation velocity, it is possible to determine the specific power of explosives and explosive compositions with sufficient accuracy. However, data on the power of TNT – RDX 70/30 markedly deviate from this plot for no good reason, possibly due to the large error of measurement of the CRZ lifetime.

Fig. 7

Dependences of the detonation velocity on the power of explosives (a) and on the Chapman–Jouguet pressure (b) (P_{C – J} = 0.0075D – 32.5). (1) TNT, (2) tetryl, (3) TNT – RDX 60/40, (4) TNT – RDX 50/50, (5) TNT – RDX 40/60, (6) TNT – RDX 36/64, (7) TNT – RDX 70/30, (8) TNT – RDX 30/70, (9) RDX.^{16, 22} PETN is pentaerythritol tetranitrate.

A similar dependence between the Chapman – Jouguet pressure and the detonation velocity is shown in Fig. 7b and can be described by the following equation:[22]

P = 0.0075 D – 32.5 (2)

Thus, an increase in the power of the explosive leads to an increase in the detonation velocity, which was first suggested by intuition and then proved by Dolmatov et al.[19]

It follows from the data of Fig. 7 and Table 4 that an acceptable yield of nanodiamonds of at least 5 mass % can be achieved if the following conditions are met:

— specific power of the explosive or a mixture of explosives ranging from 30 to 60 kJ kg^–1 μs^–1;

— detonation rate from ~ 7.3 to 8.0 km s^–1;

— detonation process ensuring a pressure of detonation products in the C – J plane between 21 and 28 GPa.

* Heat of explosion, that is, the quantity of heat released upon the explosive conversion of 1 mol or 1 kg of an explosive, is a general thermal characteristic of chemical reactions in the denotation wave front, CRZ, and reactions that continue during the adiabatic expansion of DPs until the reactions are over.

Dolmatov et al.[22] proposed approaches for predicting the yield of detonation nanodiamonds from the known value of any key characteristic of the starting explosives. The relationships between the key characteristics of explosives were determined.

Thus, for example, if the detonation velocity (usually the first characteristic of an explosive to be determined) is known, it is easy to calculate other characteristics of this explosive and the yield of DNDs.

The composition of DPs largely depends on the position of equilibrium of two reactions:

2 CO CO₂ + C

H₂ + CO H₂O + C

According to Dolmatov et al.,[22] the equilibrium of the second reaction is shifted to the right in all cases, while for the first reaction, the equilibrium is shifted to the right only for high initial densities of explosives (ρ₀ ˃ 1.5 g cm^–3). Thus, hydrogen present in explosive molecules is oxidized to H₂O, while carbon can be completely oxidized to CO₂ only for high-density charges with ρ₀ → ρ_max; otherwise, it is distributed between CO₂ and CO (for low-density charges). Decomposition of an explosive is a complex, multi-stage set of successive and parallel reactions. The course of the reactions and the composition of the reaction products may change depending on the temperature and pressure.

The yield and quality of DNDs depend on a variety of parameters:

— composition and specific power of the explosive charge;

— oxygen balance of the explosive;

— charge density;

— composition and heat capacity of the medium in the explosion chamber;

— shape of the charge;

— charge shell;

— relationship between the charge weight and volume of the explosion chamber;

— modification of the charge composition with doping elements or compounds;

— the momentum of the charge and the charge initiation site;

— design of the explosion chamber and material of the chamber wall.

In the presence of this great number of significant factors, it is clear that indication of just the same composition of explosives in different studies cannot guarantee the same yield of nanodiamonds. Moreover, the main explosion parameters for the same explosives with charges of the same density do not guarantee identical detonation velocity, pressure in the Chapman – Jouguet plane, lifetime, length (width) of the chemical reaction zone, and DND yield. These values are affected not only by the skills of the performers, but also by the availability of equipment.

However, when all parameters are optimized, the foregoing does not preclude evaluation of the expediency of using one or another explosive, which was undertaken by Dolmatov et al.[22]

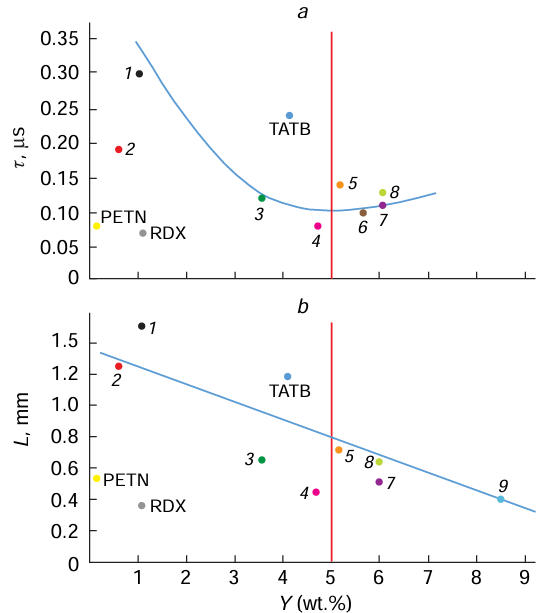
The dependence of the yield of DNDs on a number of detonation parameters is shown in Fig. 6 . The time of chemical reaction and the length of CRZ are equally important. Fig. 8a and Fig. 8b show the corresponding plots, which indicate that to achieve a DND yield of no less than 5 mass %, it is necessary that the lifetime of CRZ be in the range from 0.1 to 0.2 μs and the CRZ length be no more than 0.8 mm.

Fig. 8

Dependences of the DND yield on the time of chemical reaction (a) and the length of chemical reaction zone (b). (1) cast TNT, (2) pressed TNT, (3) pressed TNT – RDX 30/70, (4) TNT – RDX 70/30, (5) cast TNT – RDX 60/40, 1, (6) tetryl, (7) pressed TNT – RDX 40/60, (8) TNT – RDX 50/50, (9) cast TNT – RDX 60/40, 2 (the difference from cast sample 1 is in the order of preparation stages).²²

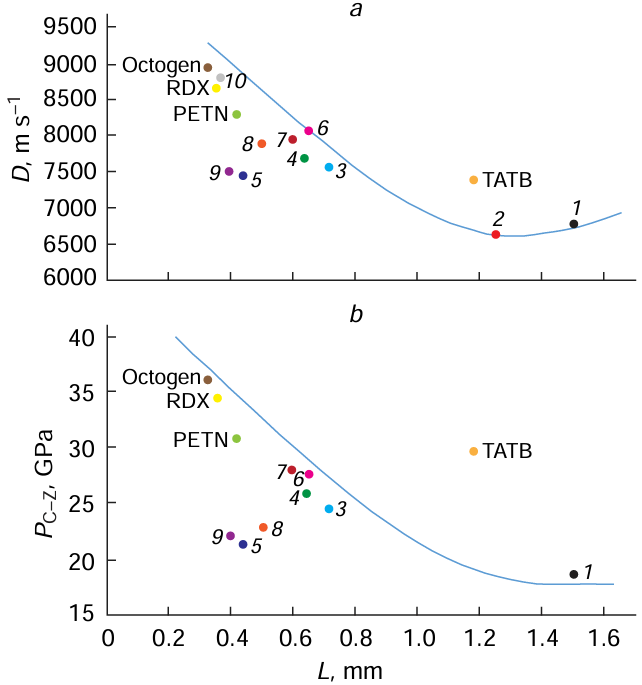
In view of the complexity and high cost of determining the detonation parameters, it is advisable to assess their mutual influence theoretically, but based on existing experimental data, which was actually done (see Table 5), in particular using data shown in Fig. 9 and Fig. 10.

Fig. 9 presents the dependences of the length of the chemical reaction zone on the detonation velocity and on the pressure in the C – J plane. Having determined the time of chemical reaction or the length of the chemical reaction zone, one can predict the yield of DNDs.

Fig. 9

Dependence on the length of the chemical reaction zone of powerful polyaromatic explosives and their mixtures with other powerful explosives present in a concentration of no less than 40 mass % on the detonation velocity (a) and on the pressure in the Chapman-Jouguet plane (b). (1) cast TNT, (2) pressed TNT, (3) cast TNT – RDX 60/40, 1 (4) TNT – RDX 50/50, (5) TNT – RDX 70/30, (6) pressed TNT – RDX 30/70, (7) TNT – RDX 36/64; (8) pressed TNT – RDX 40/60, (9) cast TNT – RDX 60/40, 2, (10) HMX/TNT 90/10.²²

Fig. 10

Dependence of the chemical reaction time on the detonation velocity (a) and on the length of the chemical reaction zone (b). (1) cast TNT, (2) pressed TNT, (3) cast TNT – RDX 60/40, (4) TNT – RDX 50/50, (5) tetryl, (6) TNT – RDX 70/30, (7) pressed TNT – RDX 40/60, (8) TNT – RDX 36/64, (9) pressed TG 30/70, (10) HMX – TNT 90/10.22.²²

Table 5 gives the elucidated dependences of the DND yields on the explosion characteristics of explosives as equations and demonstrates the relationship between the characteristics.[22]

Table 5

\[ \]

Empirical equations describing the relationship between the yield of DNDs and detonation characteristics and between various characteristics (error : ± 15%).²²

(5)

Table 6 summarizes the results of calculations based on the obtained dependences for all eight recommended polynitro­aromatic compounds: hexyl, hexanitrodiphenyl, tetranitroaniline, tetranitrobenzenes, trinitroaniline, trinitroanisole, 1,3-diamino-2,4,6-trinitrobenzene, trinitrobenzene.

Table 6

\[ \]

Explosion parameters and yields of DNDs for polynitroaromatic compounds.¹²⁶

(6)

The predicted yield of DNDs, specific power of explosives, pressure in the Chapman – Jouguet plane, and lifetime and length (width) of CRZ were calculated from the known detonation velocity.

Dolmatov et al.[126] showed that the heats of combustion (low calorific value Q_l taking into account the heat loss with water vapour) of elements and organic and inorganic compounds with a negative oxygen balance, including explosives, can be calculated by the simple relation

Q_l = 0.1387 (OB) (3)

From here, it is easy to calculate the heat еof combustion of a compound from the known gross formula.

The oxygen balance is calculated under the assumption that oxygen in the explosive molecule is fully consumed for the oxidation of hydrogen and carbon and is not released in a pure state and that the combustion and explosion give the higher oxides, carbon dioxide and water. In reality, some carbon is oxidized to carbon monoxide (CO) and, hence, less energy is released. Furthermore, experimentally determined Q_l values are not invariable: the accuracy of their determination is influenced by the method of measurements, equipment design, and the skills of the performer. In some cases, Q_l values for the same substances reported in various reference books are considerably different. In view of the ‘ideal’ nature of the OB calculation, it should be expected that the calculation of Q_l would, as a rule, give a higher value compared to the experimentally determined heat of combustion. It should be expected that the smaller the difference between the OB-based calculated Q_l value and the experimental value, the more accurate the experimental data.

A highly important characteristic of explosives is the heat of explosion Q_expl , which represents the total heat of primary chemical reactions up to the C – J plane and secondary equilibrium reactions in expanding DPs.

In the case of explosion, the heat of explosion will be less than Q_l due to incomplete redox reactions. The calculated and experimental data for explosives summarized in Table 7 [126] indicate that Q_expl is, on average, five times lower than Q_l for dinitroaromatic compounds, 1.7 times lower for trinitroaromatic compounds, and 1.05 times lower for tetranitroaromatic compounds.

Table 7

\[ \]

Dependence of the heat of combustion of explosives on the oxygen balance.¹²⁶

(7)

Thus, Q_l can be calculated with a satisfactory accuracy (± 15%) from the gross formula of the explosive, and then Q_expl can be calculated by decreasing Q_l by the required factor. From known lifetime of CRZ, W can be found by equation (1) Then the yield of DNDs is calculated from the equation

Y = 0.36 × 10^–3 W ² + 3.24 × 10^–4 W – 1.31 (4)

The details of nanodiamond formation in the detonation wave as well as the details of the kinetics of chemical reactions remain poorly understood.[127][128] This is due to exceptionally short lifetime of CRZ at supercritical temperatures and pressures. Meanwhile, compacted carbon is formed in CRZ as a precursor of DND crystallites formed beyond the C – J plane; this stimulates further interest in studying the behaviour of carbon in the chemical reaction zone.

Due to natural difficulties and the lack of appropriate equipment, experimental methods for investigation of CRZ provide semi-qualitative data, which are sometimes highly contradictory.[34][35] The problem of determining detonation characteristics in CRZ is perhaps most challenging. Nevertheless, the need to study CRZ for the applied and theoretical use of explosives makes the problem of experimental investigation of the reaction zone highly relevant.

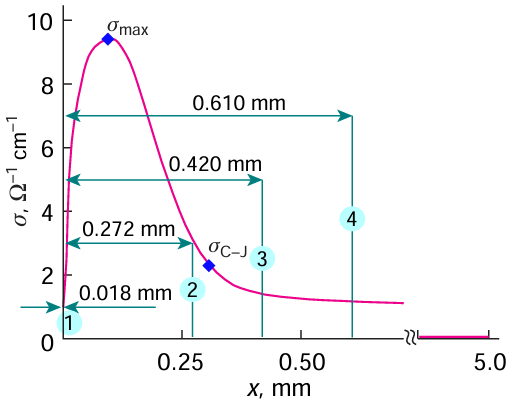
As shown in earlier studies,[31, 32][129] the electrical conductivity during detonation of an explosive of the C_aH_bN_cO_d type is determined by the content of carbon, which condenses immediately behind the detonation front and forms extended conductive structures. By measuring the conductivity of these structures, it is possible to diagnose the state of the conductive form of carbon and thus investigate the reaction zone. A typical electrical conductivity profile during detonation of a high-order explosive is shown in Fig. 11. The distribution of electrical conductivity starts with rapid growth to a maximum value. As shown previously,[28][30] [32][33] the maximum electrical conductivity σ for explosive mixtures depends on various factors, including the degree of dispersion of the components. The conductivity increase reflects the formation of conductive carbon structures that have the lowest resistance within the reaction zone. The region of high electrical conductivity correlates with the reaction zone. The decrease in σ(τ) is associated with processes in the reaction zone and reflects the the oxidation of carbon, which starts at the boundary of the structure, resulting in thinning and destruction of carbon ‘wires’ and in decreasing electrical conductivity. The lifetime of CRZ according to electrical conductivity data and, hence, the time of formation of a dense carbon structure for high-order explosives is approximately 50 ns.

Fig. 11

Dependence of the electrical conductivity σ(x) on the x-coordinate behind the charge detonation front for pentaerythritoltetranitrate with a density of 1.72 g cm^–3. σ_max is the maximum electrical conductivity, σ_{C – J} is the electrical conductivity at the end point of CRZ (Chapman – Jouguet plane).¹²⁸

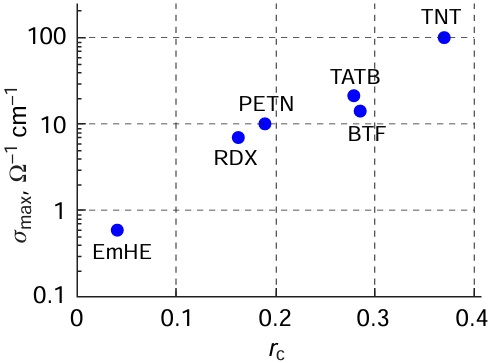
Analysis of the dependence of the maximum electrical conductivity on the carbon content in the explosive clearly indicates an increase in the conductivity with increasing carbon content (Fig. 12).

Fig. 12

Dependence of the maximum electrical conductivity σ_max found experimentally for a density close to the maximum charge density on the mass fraction of carbon r_C in the explosive molecule (EmHe is an emulsion explosive).¹²⁸

Explosives of the C_aH_bN_cO_d type have different thermodynamic characteristics and different carbon contents in their molecules. On the one hand, the greater the carbon content, the higher the amount of the potential source of nanodiamond. On the other hand, an increase in the carbon content may induce a decrease in the thermodynamic parameters and, as a result, it may happen that the compound would not reach the state needed for DND formation.

On average, nanodiamonds formed from products derived from different explosives look in the same way, but one explosive, namely BTF (C₆N₆O₆), forms products of more diverse sizes and configurations upon detonation.

To date, the understanding of processes involved in DND synthesis lags far behind their industrial implementation. A drawback is the lack of possibility of reliable characterization and unification of DNDs, which hampers their use in various fields. A natural starting point along this line is investigation of the chemical kinetics of detonation. However, determination of the kinetics of chemical reactions in CRZ is impossible due to the extreme conditions of detonation: ultrahigh temperature (3700 – 4300 K) and pressure (25 – 30 GPa), very short lifetime of the chemical reaction zone (0.1 – 0.3 μs), and many thousand reactions that take place simultaneously. However, it is possible to identify general trends that accompany the explosion, which was shown in this study. The identified and described trends make it possible to predict the yield of DNDs upon the explosion of any explosive or explosive mixture. Furthermore, the found trends give rise to the possibility of determining virtually any characteristic for an explosive on the basis of one known characteristic, which markedly simplifies the use of explosives and provides the possibility of predicting the yield of DNDs.

Subsequently, it is necessary to perform more in-depth studies of chemical and physical processes occurring during the explosive decomposition of substances, in particular to elucidate the effect of the explosive oxygen balance on the length and time of chemical reactions and pressure in the Chapman–Jouguet plane for more accurate determination of the possible yield of DNDs.

BTF — benzotrifuroxan, benzotris(1,2,5-oxadiazole 1,4,7-trioxide),

C – J — Chapman – Jouguet plane,

CS — coordination sphere,

CN — coordination number,

CRZ — chemical reaction zone in the explosive decomposition,

DDC — detonation diamond-containing carbon,

DND — detonation nanodiamond,

DPs — detonation products,

HMX — octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (octogen),

HRTEM — high-resolution transmission electron microscopy,

OB — oxygen balance of an explosive,

PA — 2,4,6-trinitrophenol (picric acid),

RDX — cyclotrimethylenetrinitramine (hexogen),

SAXS — small angle X-ray scattering,

TATB — 1,3,5-triamino-2,4,6-trinitrobenzene,

TNT — 2,4,6-trinitrotoluene,

TNT — RDX (a charge composed of TNT and RDX),

Z-TACOT — 1,3,7,9-tetranitro-6H-benzotriazolo-[2,1-а]-benzotriazol-5-ium.